Cristalización mediante autómatas celulares

(Encontrará una descripción más amplia de este tema en la Adenda del Capítulo 8 del libro de “Ciencia e Ingeniería de los Materiales” de la Editorial Paraninfo. Dicha Adenda forma parte del material digital descargable desde la página de la editorial , en la pestaña de ‘Descarga previo registro’).

Con independencia de si la nucleación se realiza bajo condiciones homogéneas o heterogéneas, el problema de la solidificación es un asunto complicado por dos razones fundamentales. Para empezar, la evolución de un grano depende de las posiciones en las que nuclean prácticamente todos los granos de la muestra y, por otra parte, el crecimiento de los granos no es lineal con el tiempo.

Dado que las interacciones entre granos son difíciles de cuantificar, y la aleatoriedad es determinante en la evolución del sistema, para la simulación se hace preciso el empleo de modelos computacionales que permitan seguir la evolución de cada grano individualmente y, al mismo tiempo, calcular propiedades globales del sistema. La técnica de los autómatas celulares es especialmente adecuada para resolver este tipo de problemas (y para otros como la propagación de infecciones, o de poblaciones de animales, que fueron los contextos en los que por primera vez se aplicó). En esta técnica la muestra a simular se supone dividida en una serie de celdillas —cuadradas o triangulares, habitualmente— cada una de las cuales se trata individualmente, pero cuyo comportamiento es dependiente de lo que le acontece a sus vecinas.

En nuestro caso, optaremos por un esquema cuadricular, en el que inicialmente todas las celdillas están en fase líquida, es decir, ninguna de ellas está cristalizada. No obstante, si se quiere introducir la naturaleza heterogénea del proceso será preciso distinguir entre dos tipos de celdillas no cristalizadas: las que tienen muy poca tendencia a cristalizar y las que tienen una significativa tendencia a hacerlo, porque, por ejemplo, contengan algún agente nucleante. Marcaremos las primeras con el número 0, y las segundas (celdillas potenciales) con -1. El número de casillas con alta tendencia a la cristalización se controlará por el usuario.

Las casillas que posteriormente vayan cristalizando serán identificadas por un número entero mayor que 1; cada uno de los cuales representará una dirección cristalográfica diferente. Cada número será representado con un color diferente, de tal modo que distinguiremos diferentes regiones, por sus distintos colores. Cada región constituye un grano del material policristalino que terminará surgiendo.

La evolución del sistema se produce porque cada celdilla del autómata debe obedecer una serie de reglas simples y estrictas, que implican a las celdillas vecinas. Consideraremos vecinas a una celdilla dada, a aquéllas que comporten una arista, esto es, cada celdilla del interior posee cuatro vecinas, ignorando, pues, las que comparten con ella únicamente un vértice. La Fig. 1 ilustra lo que decimos.

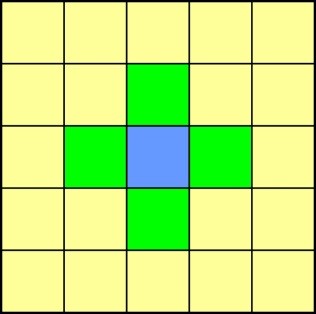
Figura 1

En cuanto a las mencionadas leyes, en nuestro caso, serán sólo tres:

  1. Una celdilla cristalizada permanece cristalizada.
  2. Una celdilla potencial no cristalizada que no tiene ninguna vecina cristalizada tiene una probabilidad de cristalizar de valor p.
  3. Una celdilla no cristalizada (incluyendo las celdillas potenciales) cristaliza si alguna de las celdillas vecinas ya está en fase cristalina. Si hubiese más de una vecina cristalizada, se elige al azar entre sus correspondientes orientaciones.

Así pues, la tarea de la simulación consiste en barrer, en cada iteración, todas las casillas del panel, consultando el estado que tenían en la iteración anterior para actualizar de acuerdo con las leyes su nuevo estado. Para simplificar el algoritmo puede ser útil sobredimensionar la matriz de estado de toda la cuadrícula con una fila adicional, por arriba y por abajo, y una columna extra, a derecha y a izquierda. Las casillas adicionales no se actualizan durante todo el proceso y permanecerán indefinidamente en el estado 0, no obstante, se gana así que las casillas situadas en los bordes puedan ser tratadas del mismo modo que las del interior.

La fracción transformada, que se calcula en cada iteración como el cociente entre el número de celdillas cristalizadas y número total de celdillas, debería cumplir en todo paso la denominada ley de Avrami.

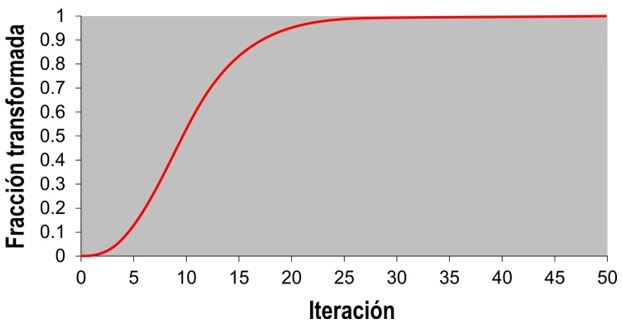
La Fig. 2 muestra el resultado de una simulación mediante la técnica de autómatas celulares, implementada con Visual Basic, de un proceso hipotético, regido por fenómenos de nucleación y crecimiento, tal como pudiera ser el caso de la cristalización.

Figura 2 Simulación de la transformación L→ S. (a) Situación intermedia, (b) situación final, (c) evolución de la fracción transformada frente al número de iteraciones (nótese la concordancia con el perfil que predice la ley de Avrami). Para esta simulación se ha empleado una cuadrícula de 250 x 250, con una concentración de celdillas potenciales del 2% y una probabilidad de 0.2.

Si la ubicación de las casillas de nucleación preferencial se limita a los contornos, entonces la situación es bien distinta. Como muestra la Fig. 3a, los granos resultantes son de tipo columnar. La Fig. 3b se ha obtenido admitiendo que los núcleos potenciales se distribuyen en bordes, pero también en el seno del líquido, lo que da como resultado la presencia de granos columnares en los bordes y equiaxiales en el centro.

Descárguese el programa que hemos preparado para ilustrar estos fenómenos y ensaye diversos valores y situaciones.

Que lo disfruten.

[Pulse aquí para descargar el programa de Cristalizador]