La resolución es un factor muy importante a considerar en microscopía, ya sea óptica o electrónica. Puede definirse como la capacidad de un sistema para producir imágenes separadas y distintas de dos puntos muy próximos. Para cuantificarla se emplea la separación mínima a la que pueden situarse dichos puntos para que la imagen resultante siga mostrándolos como objetos independientes; es decir, sin que aparezcan solapados.
Incluso en el caso de que las lentes del microscopio fuesen perfectas, el propio paso de la luz en el interior del microscopio limita su resolución. El motivo es que cuando la luz procedente de los distintos puntos de la muestra pasa a través del objetivo para formar la imagen, los puntos aparecen en dicha imagen no como puntos sino como un diagrama de anillos concéntricos conocidos como anillos o diagrama de Airy.

Cuando en el camino de una onda, como la luz, se interpone una ranura u orificio de dimensiones del orden de la longitud de onda de la emisión, se produce una distorsión de la onda denominada difracción. Los puntos de la rendija se convierten en fuentes, emitiendo ondas secundarias denominadas ondas difractadas (principio de Huygens). Para distancias no muy próximas a la apertura (distancia lo suficientemente grande como para que los rayos difractados sean paralelos), el resultado de estas ondas difractadas es lo que se conoce como difracción de Fraunhofer. La difracción de Fresnel es la que explica la difracción para distancias muy próximas al obstáculo que la produce, pero este caso no es de utilidad en microscopía óptica. El resultado de la difracción de Fraunhofer producida por una apertura circular es un patrón conocido, como se mencionó anteriormente, como diagrama de Airy. Éste está formado por un punto central (disco de Airy), que contiene el 84% de la intensidad total de la emisión, y una serie de anillos concéntricos.
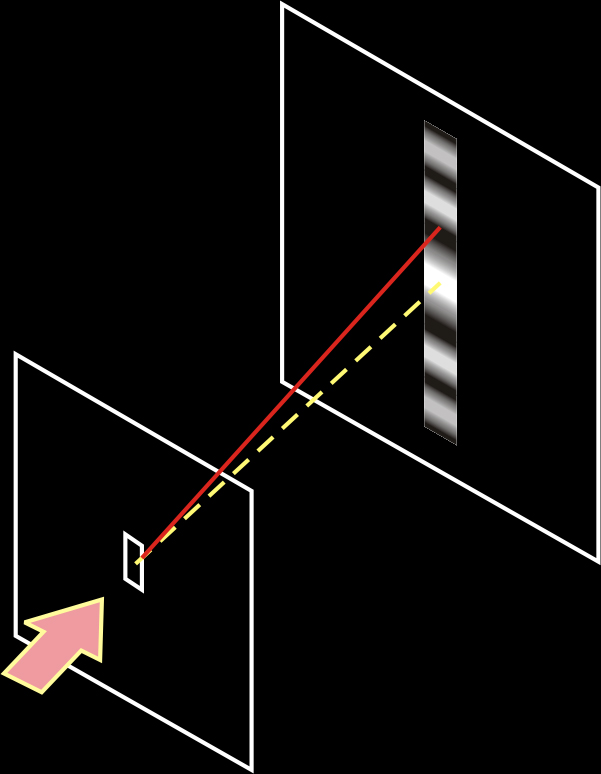
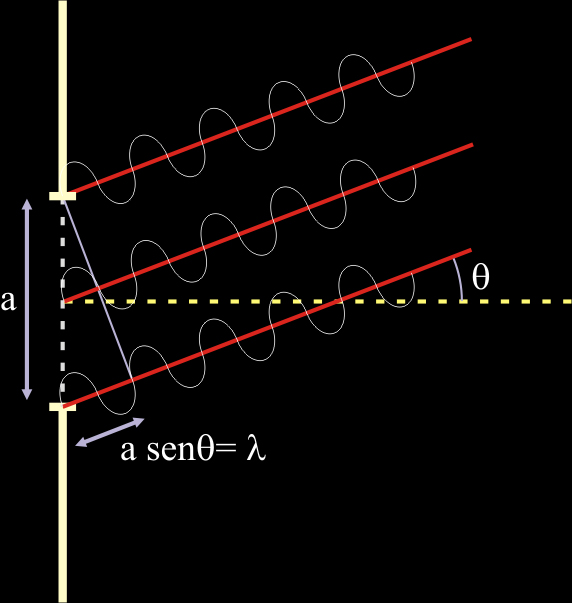
Por simplicidad, consideremos inicialmente una rendija en lugar de una apertura circular. Si la apertura tiene un tamaño a, la diferencia de caminos entre la onda situada en el extremo inferior de la rendija, y la del extremo superior es a·senθ.
 |
 |
Puede calcularse que la intensidad de la onda difractada viene dada por la expresión:
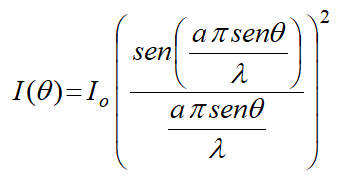
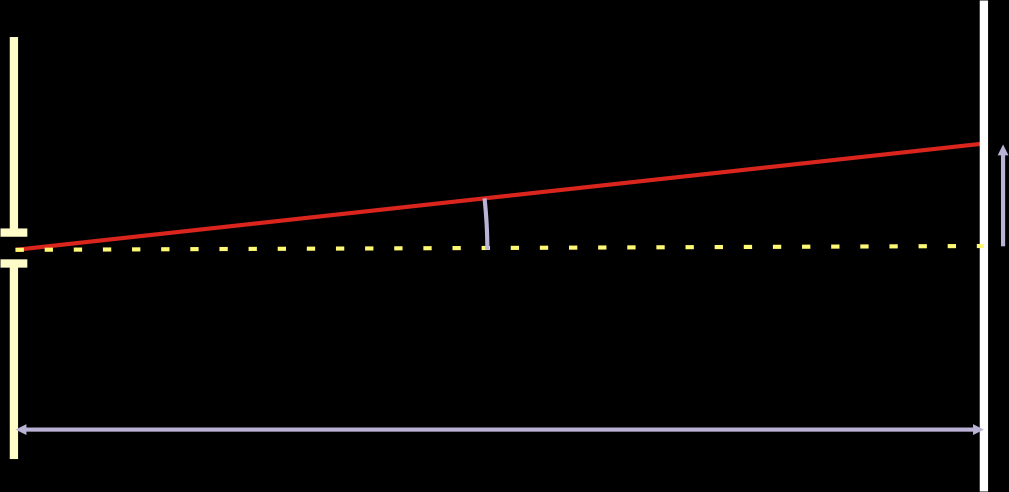
donde senθ puede aproximarse, como se muestra en la siguiente figura, por y/L, siendo L la distancia desde la apertura hasta el lugar en el que se proyecta la imagen. Por otra parte, Io es la intensidad máxima.
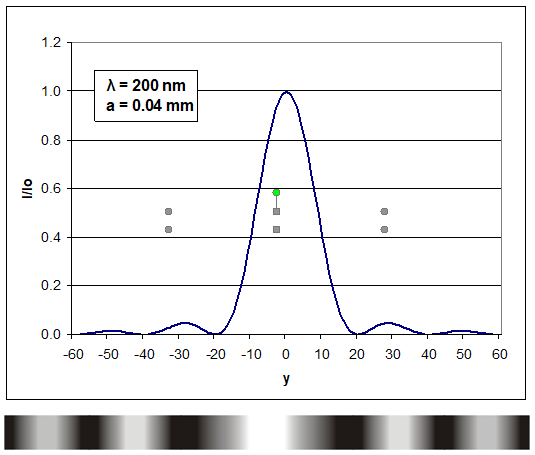
Representando gráficamente esta expresión, por ejemplo para unos valores de L=4 m y a/λ =200, se obtiene el patrón de intensidad relativa de iluminación que se forma sobre la pantalla de proyección y que se muestra en la siguiente figura.
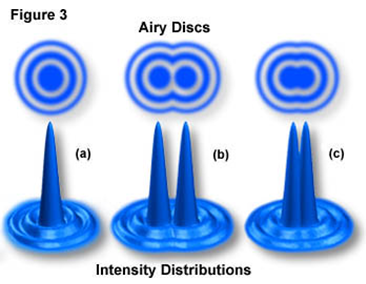
Si en lugar de una rendija, se considera una apertura circular, en lugar de obtener bandas con diferente intensidad de iluminación, tendremos anillos (anillos de Airy), tal y como se muestra en la siguiente figura.

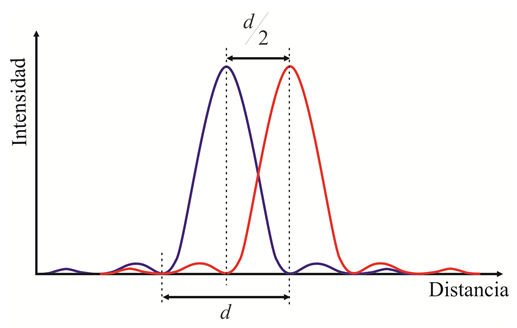
Por tanto, la luz procedente de cada una de los puntos de la muestra observada, al pasar por la apertura del objetivo, sufrirá difracción. De modo que veremos una imagen constituida por multitud de pequeños diagramas de Airy, en lugar de estar formada por puntos de luz perfectos. Los diagramas de Airy, para las distancias de proyección empleadas en microscopía, son vistos por el ojo humano como puntos, no siendo éste capaz de distinguir su forma anular. Recordemos, a este respecto, que el 84% de la intensidad total de la luz se concentra en el punto central del diagrama. Ahora bien, si dos diagramas de Airy se sitúan muy próximos entre sí, las ondas de ambos interfieren de modo que el ojo humano no es capaz de distinguirlos como dos entes independientes. La cuantificación de esa distancia mínima, o lo que es lo mismo, la cuantificación de la resolución definida al principio de este apartado, se debe a Lord Rayleigh. El criterio de Rayleigh dice que dos puntos son resolubles justo hasta que el máximo de intensidad del diagrama de Airy correspondiente a un punto, coincide con el primer mínimo de intensidad del diagrama asociado al otro punto.
donde λ es la longitud de onda de la luz empleada como iluminación, μ es el índice de refracción del medio en el cual la lente opera (1 para el aire). El producto μ senθ es normalmente denominado apertura numérica (NA).
De acuerdo con la ecuación anterior, para mejorar la resolución de un microscopio óptico (reducir r) podemos disminuir λ o aumentar su apertura numérica. La luz visible tiene unas longitudes de ondas que van desde los 750 nm (del rojo) hasta los 375 nm (del violeta). Empleando luz azul, puede reducirse la longitud de onda hasta unos 400 nm, pero este tipo de luz no es la más adecuada para el ojo humano, por lo cual es necesario incrementar la apertura numérica del microscopio para aumentar su resolución. Como máximo, usando la apertura más grande posible, senθ puede ser 1. Además, se puede aumentar el índice de refracción colocando aceite entre la muestra y el objetivo (es necesario emplear objetivos diseñados especialmente para este uso). No obstante, en la práctica no es usual encontrar objetivos con una apertura numérica mayor de 1.6 (porque senθ siempre va a ser menor que 1, y el índice de refracción de los medios que pueden emplearse rara vez supera el valor de 1.7).