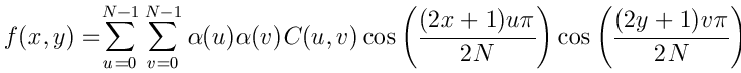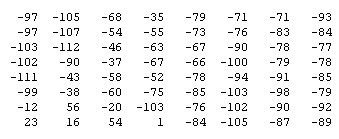El
estándar de compresión JPEG
Lo que hace a JPEG completamente diferente de otros formatos (PNG, GIF, TIFF,...)
es el hecho de aceptar la pérdida de información a la hora de comprimir. Este
tipo de compresión consta de 3 pasos.
-
Primero
se pasa la imagen del formato RGB al formato YIQ. El formato de color YIQ
representa una división entre la luminosidad (cantidad de luz percibida) y
la información sobre el color. El ojo humano es mucho más sensible a la
luminosidad que al color, cosa que se aprovecha para la compresión.
-
Después,
se realiza una transformación en la imagen mediante la transformada
discreta del coseno (TDC), que es una herramienta matemática que permite
comprimir la imagen según determinados patrones de frecuencia. Se trata de
un método de compresión con pérdida de datos.
-
Por
último, se codifica el conjunto de datos obtenidos al aplicar la TDC,
usando un método que no producen pérdida (código de Huffman).
Para
recuperar la imagen se usa el proceso inverso de transformación de imágenes.
Formatos
de color RGB e YIQ.
En el formato de color RGB, las imágenes a color se almacenan en 3 canales
independientes (rojo, verde y azul) que toman valores de 0 a 255 dependiendo de
la intensidad.
El formato de color YIQ representa una división entre la luminosidad (Y) y el
color (I, Q). La conversión entre RGB e YIQ es:

El ojo
humano es menos sensible a los matices de color que a la cantidad de luz
percibida. Es por ello que podemos reducir la información almacenada para los
canales I y Q de una imagen YIQ, por ejemplo, a
la mitad: si tenemos una imagen 8 x 8 en formato YIQ, la reduciremos a un canal
Y de 8 x 8 y un canal I y otro Q de 4 x 4. Para calcular los valores nuevos de
estos canales podemos hallar la media aritmética de los valores de cada 4
píxeles.
En este
paso se produce pérdida de la información, como podemos ver en el siguiente
ejemplo:

Este es un
trozo de imagen original y comprimida JPG, ampliadas para ver las diferencias.
Como vemos, los colores rojo y azul en la imagen original se han visto alterados
en la imagen JPG.
Para
evitar este efecto no deseado, algunos programas como Paint Shop Pro, ofrecen
este paso de manera opcional en la compresión JPG. De esta forma, los colores
no se ven tan degradados y la imagen original y comprimida son prácticamente
iguales:

Transformada
discreta del coseno
Las
transformadas de una imagen generan conjuntos de datos que contienen la misma
información que las imágenes originales, con la propiedad de poder volver a
generar las imágenes originales mediante las correspondientes transformadas
inversas.
Una imagen monocolor de dimensiones N x N, se puede expresar como una función
de dos variables f(x,y) donde (x,y) son las coordenadas de cada píxel
(x=0,1,...,N-1 e y=0,1,...,N-1) y f(x,y) es la intensidad de color del píxel (x,y).
La
transformada discreta del coseno consiste en calcular otra matriz F a partir de
la anterior.
El dominio
de F es el mismo que el de f.
Para cada
valor (u,v) con u=0,1,2,...,N-1 y v=0,1,2,...,N-1, tenemos que

La inversa de la transformada tiene por fórmula:
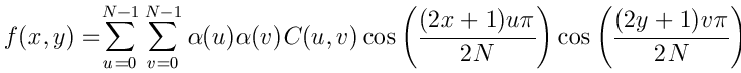
para
x=0,1,2,...,N-1 e y=0,1,2,...,N-1 y

En forma
matricial, C=MFMT donde


que, de
forma aproximada, es:

Ejemplo:
Consideremos
la siguiente imagen I y la matriz asociada A:

La
transformada discreta del coseno de A,
C, es una nueva matriz de las mismas dimensiones que la anterior:

Como
podemos observar, los valores mayores se encuentran en la parte triangular
superior-izquierda de la matriz.
Si
calculamos la inversa de la transformada del coseno a la matriz anterior,
obtenemos la misma matriz que la original:

Para
almacenar la matriz C se realiza un proceso de normalización, es decir, se
busca una función N(u,v) tal que
C*(u,v)=Redondeo(F(u,v)/N(u,v))
sea una
matriz con "muchos" ceros. Esta nueva matriz, C* es la que
se almacena en el siguiente paso.
Para poder
aplicar la TDC según el estándar JPEG, debemos dividir la imagen original en
matrices cuadradas de 8 x 8 píxeles.
Cada
matriz C de 8 x 8 píxeles obtenida aplicando la TDC a cada subimagen de
dimensión 8 x 8 se aproxima por otra más sencilla C* mediante
un proceso de normalización.
En este
paso es donde radica la pérdida de información. Dependiendo de cómo
normalicemos C*, conseguiremos comprimir más pero, a la vez, perder más
información.
JPEG
recomienda una matriz de normalización estandarizada para las imágenes con 256
niveles de intensidad, que es:

Aplicando
esta normalización a nuestro ejemplo obtenemos la nueva matriz:

que, como
vemos tiene muchos ceros en la parte triangular inferior-derecha.
En la
mayoría de los casos, los programas que han implementado el método JPG, antes
de realizar la TCD, realizan una traslación en los colores de la imagen para
pasar de [0,255] a [-128,127]. De esta forma se consigue
que los colores esté distribuidos alrededor del cero. El único cambio
que se produce en realidad, es el primer elemento de la matriz transformada. En
el ejemplo la matriz original que resulta después de restar 128 a todos sus
elementos es:
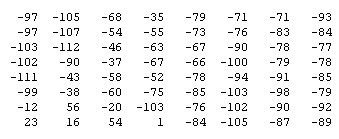
Y la
matriz que resulta al realizar la transformada y normalizar:

Como
vemos, la única diferencia con la matriz normalizada de la matriz original es
el primer elemento (ahora vale -35 y antes 29).
Algoritmo
de Huffman
Para almacenar la imagen normalizada, se sigue un recorrido en zig-zag para
obtener una lista con los ceros acumulados al final. Se usa el código de
secuencia para codificar la lista.
Ahora,
usamos el algoritmo de Huffman que se basa en utilizar el menor espacio posible
en bits para aquellos caracteres más repetidos.
Aunque podemos utilizar una compresión de Huffman propia, existe unas tablas
estandarizadas que nos permiten obtener el código de Huffman para cualquier
valor.
En nuestro
ejemplo, la lista sería
29,
9,-7,5,-12,-4,-6,-5,6,-3,2,-2,1,1,-1,0,1,0,0,1,0,0,0,-1,1,0,1,0,0,0,1,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,F
Con la
letra F (de fin) indicamos que desde ese elemento hasta el final de la lista son
todos ceros (hasta completar los 64 elementos de la lista).
El
siguiente paso sería almacenar cada lista de cada subimagen 8 x 8 de la imagen
usando algún algoritmo que elimine la redundancia de código, como el algoritmo
de Huffman. En este paso radica la propiedad de almacenar usando distintos
grados de compresión. Si almacenamos cada lista con los 64 elementos, el grado
de compresión sería pequeño. Cómo los datos significativos están al
principio de la lista, podríamos considerar sólo los primeros elementos de la
lista (por ejemplo, los 16 primeros), y en este caso, el grado de compresión
sería mayor.
Descompresión:
transformada inversa del coseno
Para
descomprimir la imagen, hemos de descodificarla para obtener la matriz
normalizada C*(u,v).
Deshacemos
la normalización: F*(u,v)=C*(u,v)N(u,v), donde N era la
matriz de normalización, y ahora aplicamos la transformada inversa de F*mediante
la fórmula.
En nuestro
ejemplo, la matriz obtenida tras este proceso es:

Redondeamos,
para obtener una matriz de enteros, y la matriz descomprimida sería:

La
diferencia entre la matriz original y la descomprimida es: