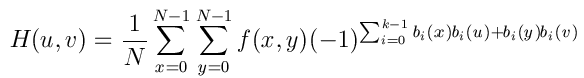
La transformada de Hadamard
A diferencia de la transformada de Fourier, que se basa en términos trigonométricos, la transformada de Hadamard consiste en un desarrollo en serie de funciones básicas cuyos valores son +1 o -1.
La transformada de Hadamard, H(u,v), de una imagen f(x,y) de dimensiones N x N donde N=2k viene dada por la fórmula
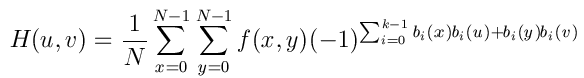
donde u=0,1,...,N-1 y v=0,1,...,N-1 y bj(z) es el j-ésimo bit de la representación binaria de z.
La transformada inversa de Hadarmad es idéntica a la anterior, intercambiando las funciones H y f.

La ventaja que tiene esta transformada es que cualquier algoritmo que calcule la transformada directa de Hadamard, puede emplearse sin modificaciones para calcular la transformada inversa.
Los núcleos de la transformada de Hadamard también son simétricos y separables.
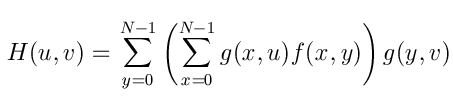
donde

Por tanto para calcular la transformada de Hadamard bidimensional, se calcula dos veces consecutivas la transformada de Hadamard unidimensional:

Llamemos g(x,u) al núcleo de esta transformada. Es muy fácil calcular la matriz del núcleo para cualquier N=2k de forma inductiva.
La matriz de Hadamard, de menor k, es
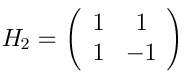
Inductivamente,

La matriz de transformación A tal que H=AFA, donde F es la imagen original, viene dada por A=(1/(N1/2))HN.
Por ser A-1=A, la formulación de la transformada inversa es idéntica a lo anterior.
Ejercicio:
Calcular los valores de g(z,w) para N=4
Comprobar que la matriz G que representa la función g(z,w) es simétrica con filas y columnas ortogonales.
Diseñar un algoritmo que calcula la transformada de Hadamard de una imagen usando la matriz anterior.
Para practicar: