Momentos
1 Introducción.
El procesamiento de imágenes es un proceso que comprende una serie de pasos:
1. Capturar la imagen. Es importante conocer como ha sido capturada la imagen para tomar decisiones sobre el tratamiento de la imagen.
Digitalización. Esta fase es la que permite que la imagen aparezca en la pantalla y está íntimamente relacionada con la fase anterior.
Procesamiento de la imagen. Consiste en mejorar la imagen modificando, si fuera necesario, el contraste, el brillo, etc. Normalmente, los algoritmos que realizan estas operaciones son sencillos.
Restauración. A menudo, esta etapa consiste principalmente en la eliminación de ruidos. Implica un conocimiento de la imagen.
Analizar e identificar la imagen.
El elemento fundamental de la pantalla es el píxel y en el se basará la aplicación para hacer los cálculos de momentos. La pantalla se representa mediante una matriz en la que cada elemento es un píxel. Por lo tanto, la representación que se usará es la matricial. El píxel ocupa un área, por lo tanto, se considera que el proceso de digitalización se ha realizado bien si un píxel es un rectángulo cuyo valor es la media de la radiación que llega a su rectángulo.
La unión de todos los píxel se denomina grid, existen tres posibles tipos de grid, que aunque la aplicación no los tenga en cuenta y solo use uno de ellos, no está demás citarlos.
- Triangular.
- Rectangular.
- Hexagonal.
La aplicación solo tendrá en cuenta dos posibles valores en un píxel, 1 o 0, o bien encendido o apagado, obviamente, las integrales que se usan para calcular momentos, en este tipo de imágenes, es decir, imágenes digitales, se convertirán en suma, lo cual facilita bastante el calculo. Sería posible tener en cuenta los distintos tonos o colores que puede tomar un píxel, pero los cálculos de momentos se complicarían bastante, aunque el reconocimiento de imágenes sería más exacto.
Los momentos son propiedades numéricas que se pueden obtener de una determinada imagen. El uso de momentos permite conocer bastante información de una imagen y tiene la ventaja de que no solo usa los bordes de una figura, sino que tiene en cuenta todos los píxeles de la misma. Se usan principalmente para reconocer una forma en una imagen.
2 Momentos Geométricos
2.1 Momentos Simples.
La teoría de los momentos proporciona una interesante y útil alternativa para la representación de formas de objetos. Si tenemos un objeto en una región a que viene dado por los puntos en los que f(x,y)> 0, definimos el momento de orden p,q como:
mpq = òò xp yq f(x,y) dx dy para p,q = 0,1,2,...
El teorema de representación de los momentos nos dice que el
conjunto infinito de momentos ![]()
mp,q, p,q=0,1,...![]()
determinan unívocamente f(x,y) y viceversa. Tendremos una imagen digital definida por
la función f(x,y), donde (x,y) son las coordenadas de un punto y f(x,y), el valor de ese punto; en el caso del aplicativo
desarrollado, este valor será 0 si el punto es distinto de negro y 1 si es
negro; si se hubieran tenido en cuenta los colores en una imagen este valor
dependería del color del punto. Como se ha comentado anteriormente, al tratarse
de imágenes digitales, el momento de orden (p+q) se
define ahora como:
M(p,q) = åxåy xp yq f(x,y)
2.2 Momentos Centrales.
La aplicación más útil de los momentos son las funciones que podemos extraer de ellos, que son invariantes a transformaciones geométricas tales como traslación escalado y rotación. Los momentos centrales se usan para reconocer una imagen independientemente de su situación en un eje de coordenadas. Por ejemplo, la imagen de la Forma no sería igual que la imagen de la Forma Centrada, sin embargo, lo que es la figura en sí, es la misma. Para calcular los momentos centrales se usa el centroide de la figura.
Para calcular los momentos centrales se usa:
mpq = òò (x-X)p (y-Y)q f(x,y) dx dy
MCpq = ååò (x-X)p (y-Y)q f(x,y)
Y para calcular el centroide se usan los momentos de orden 1 y de orden 0.
X = M(1,0) / M(0,0) Y = M(0,1) / M(0,0)
El centroide o centro de masas de una figura viene determinado por las coordenadas (X,Y), de forma que el área de la figura que queda a la derecha e izquierda del punto X es la misma, al igual que el área que queda por encima y por debajo del punto Y.
2.3 Momentos Centrales Normalizados.
Si con los momentos simples obteníamos el área de una figura y por lo tanto no importaba si esta estaba invertida por ejemplo, para reconocerla; y con los momentos centrales distinguíamos una figura no importando si estaba desplazada; ahora con los momentos centrales se podrán reconocer figuras dentro de una imagen independientemente de su tamaño. Es decir, en nuestro ejemplo, la estrella ampliada es una estrella igual que la estrella normal y seguirá siendo una estrella por mucho que se amplíe o se reduzca.
MCN(p,q) = MC(p,q) / MCβ(0,0)
Donde:
β = ((p + q) / 2) + 1
2.4 Momentos de Orden 0.
Momentos Simples de Orden 0. M(0,0): Suma todos los píxeles cuyo valor es uno, es decir los que son distinto de blanco, por lo tanto calcula el área.
El momento simple de orden 0 representa el área de la figura en imágenes binarias y la superficie en imágenes en escala de grises. Es la suma de los valores de todos los píxeles. Para ello nos basamos en la fórmula de los momentos simples.
![]()
2.5 Momentos de Orden 1.
Momentos Simples de Orden 1, M(1,0), M(0,1): Como hemos comentado anteriormente se usan principalmente para hallar el centro de masas de una figura.
![]()
![]()
Momentos Centrales de Orden 1, MC(1,0), MC(0,1): Estos momentos son 0 por definición.


Momentos Centrales Normalizados de Orden 1, MCN(1,0), MCN(0,1): Estos momentos son 0 por definición.
2.6 Momentos de Orden 2.
Es donde comienza el análisis de las imágenes mediante el reconocimiento de formas, son de vital importancia en el calculo los momentos centrales. La densidad de la figura se multiplica por distancias al cuadrado desde el centro de masas o centroide (Inercia).
![]()
Momentos Centrales de Orden 2.
MC(2,0): Su valor aumentará cuanto mayor sea la componente horizontal de una figura.
MC(0,2): Su valor aumentará cuando mayor sea la componente vertical de una figura.
MC(1,1): Usa las componentes Horizontal y Vertical. Puede ser positivo o negativo dependiendo de donde se encuentre la componente vertical; si la componente vertical se encuentra en los cuadrantes 2º y 4º, entonces será negativo, si por el contrario está en los cuadrantes 1º y 3º entonces será positivo. Teniendo en cuenta esto es fácil deducir que una imagen simétrica respecto a los ejes, el MC(1,1) será 0.
Matriz de Rotación: Los momentos centrales forman las componentes de la matriz de rotación, partiendo de estas componente se obtendrán tanto el Angulo de Rotación como la Excentricidad.
| MC(0,2) -MC(1,1) |
| -MC(1,1) MC(2,0) |
Angulo de Rotación: Se define como el ángulo entre el eje de abscisas y el eje alrededor del cual la figura puede rotar con mínima inercia.
Excentricidad: Si definiéramos una elipse que rodease la figura para que quedase fuera un área de la figura igual al área que quedase dentro de una elipse, y teniendo en cuenta que una elipse tiene 2 focos, la excentricidad se definiría como la distancia entre los dos focos. La excentricidad medida sobre figuras normalizadas se encuentra en un rango entre 0 y 1. Por ejemplo para un cuadrado la excentricidad resulta 0, lo mismo que para un circulo ya que la elipse coincide con el circulo, en cambio para una recta infinita, la excentricidad sería infinita y si estuviera normalizada entonces sería 1.
2.7 Momentos de Orden 3.
![]()
Estos momentos sirven para calcular los momentos invariantes. A partir de los
momentos centrales normalizados de orden 2
y 3 se obtienen los siete momentos invariantes. Estos momentos, como su
propio nombre indica, se mantienen invariantes ante rotaciones, traslaciones y
cambios de escalas de una figura concreta
![]()
![]()
![]()

![]()

2.8 Conclusiones.
Debido a los errores que se producen en el tratamiento de las imágenes, la resolución de las imágenes y la propia naturaleza digital de los datos, se producen una serie de errores en los cálculos. Se han usado imágenes en blanco y negro y procurando que no tengan ruido para obtener información más clara y con menos margen de error.
Una posterior versión de este aplicativo podría tener en cuenta las distintas gamas de colores, de esta forma se obtendría un reconocimiento más fiable; y si además se añadirá una aplicación de eliminación de ruidos, se podría obtener un programa con más estabilidad que el presentado en este trabajo.
Aplicaciones:
–Construir una base de datos de momentos geométricos y emplearla como patrones para el reconocimiento de formas (aviones en vuelo,flores,peces,etc).
3 Momentos de Legendre
La utilización de los momentos de Legendre en la manipulación de imágenes surge con la
necesidad de nuevas aplicaciones, siendo la más importante de ellas la
reconstrucción de una imagen a través de las características matemáticas que
nos proporcionan los momentos.
La reconstrucción mediante el uso de
los momentos geométricos es muy costosa y sobre todo propensa a grandes errores
de cálculo, lo cual la hace prácticamente inviable y poco fidedigna.
Los momentos de Legendre de orden (p,q) se definen por:
![]()
donde el polinomio de Legendre de orden p viene dado por:

El momento de Legendre de orden p,q generaliza el momento geométrico del mismo orden en el sentido que el monomio x^p, y^q se sustituye por el polinomio ortogonal Pp(x)Pq(y) del mismo orden.
Como anteriormente hicimos, podemos aproximar la versión continua del cálculo de momentos a otra discreta mediante el uso de sumatorios.
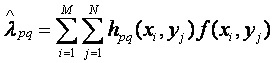

Donde
Sin embargo, esta versión de la fórmula es difícilmente computable y se sustituye por la siguiente:


El valor de f(x,y) estará comprendido en el intervalo [0,255] y el de x e y en un cuadrado de lado [-1,1], lo cual nos obliga a hacer un cambio de variable para que los puntos de la imagen se adecuen a este intervalo.
La computación de los momentos de Legendre es muy costosa, lo cual induce a introducir serias modificaciones en cuanto a lo que eficiencia se refiere. Además está el hecho de que en muchas ocasiones es necesario el cálculo de momentos de un nivel alto. A todo esto se une la necesidad de mantener el nivel de error en un término muy pequeño, así como trabajar con aritmética de grandes números.
3.1 Reconstrucción de imágenes a través de los momentos de Legendre
La reconstrucción de imágenes mediante el uso los momentos geométricos, expuestos en primera instancia está sujeta a múltiples inexactitudes, unido a una complejidad computacional alta.
El uso de los momentos de Legendre hace posible reconstruir una imagen a partir de las características numéricas de ésta que se obtienen.
El problema que se plantea es: ¿cómo reconstruir una imagen si solo disponemos de un conjunto finito de momentos.?
Los polinomios de Legendre Pp(x) son un conjunto completo ortogonal establecido en el intervalo [-1,1]

donde ![]() es la función de Kronecker, tal que
es la función de Kronecker, tal que ![]() = 1 si p=q y 0 en otro caso
= 1 si p=q y 0 en otro caso
Entonces, como f(x,y) es continua sobre la imagen plana, se puede escribir la función de imagen f(x,y) como una expansión de series infinitas truncada al momento de orden máximo que consideremos, y usando la versión aproximada de los momentos de Legendre:

En cuanto al error que se produce en la reconstrucción de imágenes mediante momentos de Legendre, se mantiene en un nivel bajo tolerable.
Los resultados experimentales indican que cuando el orden dado (Mmax) alcanza un cierto valor, la función obtenida es muy parecida a la original f(x,y).
3.2 Resultados experimentales
Hemos tratado un conjunto de imágenes en blanco y negro de 150x150 píxeles y el cálculo hasta momentos de orden 20 y una precisión de coma flotante de 28 decimales, de las cuales hemos podido obtener los siguientes resultados:
- Duración del cálculo de momentos hasta orden 20:
- Duración de la reconstrucción:
Todo ello bajo una máquina a 1.5 Ghz con 384 Mb de RAM
- Se obtienen mejores resultados cuanto mayor es la imagen, pero encareciendo así considerablemente el tiempo de cómputo.
- Cuanto más píxeles negros tenga una imagen mejor
- Cuanto más rectas las líneas mejor
- Sería necesario una/s máquina/s de gran potencia de cálculo así como aumentar el número de momentos para obtener resultados fieles a las imágenes originales
- Es completamente esencial trabajar con aritmética de grandes números
- Hay que utilizar el máximo tamaño posible de decimales en la mantisa de los números flotantes
3.3 Ejemplos de aplicación de los momentos de Legendre a la reconstrucción de imágenes
|
Imagen Original
n = 3
n = 10
n = 20 |
|
Imagen Original n
= 3
n = 10
n = 20 |







