
La transformada de Fourier
La transformada de Fourier de una función continua e integrable de una variable real x se define por

Observemos que la transformada de una función real es una función compleja. Es decir, F(u)=R(u)+I(u)i, donde R(u) e I(u) son la parte real e imaginaria de F(u), respectivamente.
La variable u recibe el nombre de variable de frecuencia.
El módulo de F(u), |F(u)|= (R(u)2+ I(u)2)1/2 recibe el nombre del espectro de Fourier.
El cuadrado del espectro se denomina espectro de potencias o densidad espectral de f(x).
Su ángulo P(u)=arctg(I(u)/R(u)) recibe el nombre de fase.
La inversa de la transformada se define como:
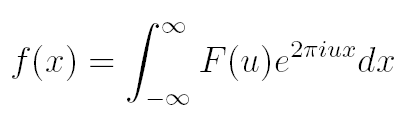
Análogamente, se define la transformada de Fourier de una función continua e integrable de 2 variables:

y su inversa como

Transformada de Fourier discreta
Sea f(x,y) una imagen en niveles de grises, tal que x=0,1,...,N-1 e y=0,1,...,N-1; y f(x,y) toma valores discretos representando el nivel de gris del píxel (x,y) entonces, la transformada discreta de Fourier de la imagen consiste en una función F(u,v) tal que u=0,1,...,N-1 y v=0,1,...,N-1:

y su inversa como

En este apartado, nos vamos a centrar en las propiedades de la transformada de Fourier discreta bidimensional (TFD).
Esta propiedad de la TFD esta relacionada con la posibilidad de calcular la TFD de una función bidimensional como una combinación de dos transformadas Fourier discretas, calculando primero una TFD sobre la variable de uno de los ejes y al resultado aplicarle de nuevo la TFD sobre la variable del otro eje.
La ventaja que aporta esta propiedad es el hecho de poder obtener la transformada F(x,y) o la inversa f(x,y) en dos pasos, mediante la aplicación de la Transformada de Fourier 1-D o su inversa:

donde

Por tanto, la transformada de la matriz f(x,y) se ha realizado, calculando primero la transformada unidimensional a cada una de sus filas y multiplicando el resultado por N. Posteriormente, se calcula la transformada a cada una de las columnas de la matriz F(x,v)
La transformada de Fourier y su inversa son transformaciones lineales, es decir, poseen la propiedad distributiva respecto de la suma.
Tanto la transformada discreta de Fourier como la transformada inversa, son periódicas de periodo N.
Un caso particular de esta propiedad consiste en mover el origen de la transformada de Fourier de f(x,y) al centro de la matriz N X N que le corresponda, es decir al punto (N/2,N/2). Para ello, podemos hacer uso de que:
f(x,y)(-1)x+y se hace corresponder con F(u-n/2,v-N/2)
También cabe resaltar, que un desplazamiento en la función f(x,y), no provocará un cambio en la magnitud de su transformada de Fourier. Véase esto matemáticamente en la siguiente expresión:
![]()
La transformada de Fourier de una función f(x,) es real es simétrica conjugada. Esto provoca que:
|F(u,v)|=|F(-u,-v)|
Por tanto, gracias a esta propiedad de simetría, para calcular la magnitud de los puntos de un periodo completo, tan sólo necesitamos calcular los N/2+1 primeros puntos, siempre y cuando el origen de la transformada este centrado en el punto (N/2,N/2).Para conseguir este movimiento del origen en la transformada, podemos aplicar la propiedad de traslación.

Si rotamos la función f(x,y) un ángulo determinado, la transformada de Fourier también será afectada por una rotación del mismo ángulo. Esta propiedad también se da a la inversa, es decir, si la transformada se rota en un determinado ángulo, la transformada inversa también se verá rotada ese mismo ángulo.

Una definición ampliamente utilizada del valor promedio de una función discreta de dos dimensiones es:

Esta expresión se puede calcular a partir de la transformada de Fourier, sin más que sustituir en la función F(u,v) para el punto (0,0).Por tanto, el valor promedio se puede expresar matemáticamente en función de la transformada de Fourier, como sigue:

El espectro de Fourier suele tener un rango mucho mayor que los usuales para mostrar una imagen. Una técnica usual para evitar esto es considerar el logaritmo del espectro usando la fórmula
D(u,v)=C(log(1+|F(u,v)|))
donde C es una constante adecuada de reescalado de la imagen, que se aplica para obtener valores dentro de la paleta de colores disponible.

|
Forest Texture |
|
|
Mud Texture |
|
|
Field Texture |
|
|
Pond Texture |
|
|
Village Texture |
|
|
Water Texture |
|
Para practicar: