[1943] McCulloch y Pitts propusieron modelos neuronales que implican transiciones repentinas 0-1 y 1-0 en el estado de las neuronas. Estos resultados sirvieron de base para el modelado de sistemas neuronales.

[1949] Hebb utilizó modelos matemáticos para abordar el concepto del aprendizaje mediante el refuerzo y la asociación.

[1957,1962] Rosenblatt idea un tipo de sistemas denominados máquinas de aprendizaje (perceptrones) que ponían en práctica la teoría del reconocimiento de patrones. Se demostró que al entrenar los perceptrones usando conjuntos de entrenamiento linealmente separables se obtenía una solución en un número finito de iteraciones que conseguía separar correctamente las clases representadas por los patrones del conjunto de entrenamiento.

Las expectativas se desvanecieron pronto ya que estos avances eran insuficientes para la mayoría de las tareas de reconocimiento de patrones de significación práctica.

[1965] Nilsson resumió el estado de las investigaciones en el campo de las máquinas de aprendizaje.

[1969] Minsky y Papert presentaron un análisis muy desalentador sobre la limitación práctica de las máquinas de tipo perceptrón.

[1986] Rumelhart, Hinton y Williams desarrollaron nuevos algoritmos de entrenamiento para perceptrones multicapa. Para ello usaron el método conocido como regla delta generalizada para el aprendizaje por retropropagación. Dicha regla se ha podida aplicar en algunos problemas de interés práctico. Por este motivo, las máquinas de tipo perceptrón multicapa constituyen uno de los principales modelos de redes neuronales en uso.

2. Introducción.

Si nos pidiesen calcular la raíz cuadrada de 5 con tres decimales de precisión y sin usar calculadora ni lápiz ni papel diríamos que no somos capaces de realizarlo. Sin embargo, esta tarea es una operación rutinaria y muy sencilla para un ordenador. No obstante, tareas como coger una moneda al vuelo que lanzamos al aire o reconocer una cara en una fotografía que son acciones cotidianas para nosotros son tareas realmente duras para un ordenador. Es decir, tareas de reconocimiento de patrones, control de dispositivos, clasificación de objetos, etc. que suponen gran cantidad de cálculo y tiempo para un ordenador pueden ser realizadas de forma instantánea por un ser vivo, no necesariamente un ser humano.

Ejemplo: El sonar de un murciélago.

El murciélago debe determinar la velocidad relativa, tamaño y la posición del obstáculo a través de su sonar. Todo el proceso de extracción de información ocurre en un cerebro del tamaño de un garbanzo en un tiempo que es la envidia de los ingenieros que trabajan en sonar y radar.

De estas observaciones nos surge la cuestión que va ha suponer el nacimiento de las Redes Neuronales Artificiales o ANS (Artificial Neural Systems).¿Qué parámetros hacen posible la supremacía del cerebro en unas determinadas tareas frente a las computadoras?.

Curiosamente, las neuronas son mucho más simples, lentas y menos fiables que una CPU, y a pesar de ello, existen problemas difícilmente abordables mediante un computador convencional que el cerebro resuelve eficazmente (reconocimiento del habla, visión de objetos inmersos en ambiente natural (Ver figura 1), respuestas ante estímulos de entorno, etc.).

Por lo tanto, la idea que subyace en los ANS es que para abordar el tipo de problemas que el cerebro resuelve con eficiencia, puede resultar conveniente construir sistemas que simulen la estructura de las redes neuronales biológicas con el fin de alcanzar una funcionalidad similar.

Figura 1. Ilustración de una trama compleja.

La ilustración anterior corresponde a un dálmata visto de perfil, mirando hacia la izquierda, con la cabeza baja para olfatear el terreno. Con ello se pretende mostrar la complejidad que supone el crear aplicaciones para reconocer objetos de la imagen.

Dado que el perro se ha mostrado como una serie de manchas negras sobre fondo blanco, ¿cómo se puede escribir un programa de computador para determinar precisamente qué manchas forman el contorno del perro, qué manchas se pueden atribuir a manchas de la piel y qué manchas son simplemente estorbos?. E incluso podríamos plantearnos una cuestión de mucho más interés como es: ¿Cómo es que nosotros podemos ver rápidamente el perro que hay en la ilustración, mientras que un computador no es capaz de hacer esta discriminación?.

3. Redes Neuronales Biológicas.

Se estima que el sistema nervioso contiene alrededor de cien mil millones de neuronas, organizadas mediante una red compleja en la que las neuronas individuales pueden estar conectadas a varios miles de neuronas distintas. Se calcula que una neurona del córtex cerebral recibe información, por término medio, de unas 10.000 neuronas, y envía impulsos a varios cientos de ellas.

Desde un punto de vista funcional, las neuronas constituyen procesadores de información sencillos. Como todo sistema de este tipo, posee un canal de entrada de información, las dendritas; un órgano de cómputo, el soma, y un canal de salida, el axón (Fig. 2).

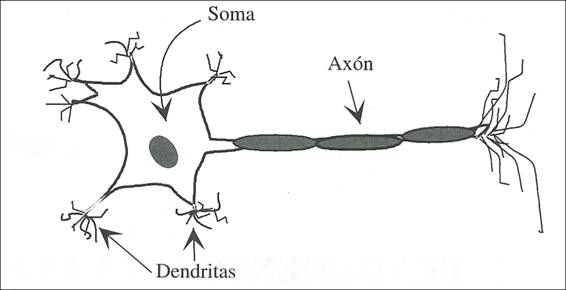
Figura 2. Estructura de una neurona biológica típica.

La mayor parte de las neuronas poseen una estructura de árbol llamada desdirías de tal forma que las neuronas se unen a través de uniones denominadas sinapsis. En el tipo de sinapsis más común no existe un contacto físico entre las neuronas, sino que éstas permanecen separadas por un pequeño vacío de unas 0.2 micras. Con relación a la sinapsis, se habla de neuronas presinápticas (las que envían las señales) y neuronas postsinápticas (las que las reciben). Las sinapsis son dirigidas, es decir, la información fluye siempre en un único sentido.

4. Estructura de un ANS.

Los tres conceptos a emular de los sistemas nerviosos son: paralelismo de cálculo, memoria distribuida, y adaptabilidad al entorno:

El procesamiento paralelo resulta esencial en este tipo de tareas para poder realizar gran cantidad de cálculo en un intervalo de tiempo lo más reducido posible.

Otro concepto importante que aparece en el cerebro es el de memoria distribuida. Mientras que en un computador la información ocupa posiciones de memoria bien definidas, en los sistemas neuronales se encuentra distribuida por las sinapsis de la red, de modo que si una sinapsis resulta dañada, no perdemos más que una parte muy pequeña de la información.

El último concepto fundamental es el de adaptabilidad. Los ANS se adaptan fácilmente al entorno modificando sus sinapsis, y aprenden de la experiencia, pudiendo generalizar conceptos a partir de casos particulares.

A partir de las tres propiedades anteriores concluimos que en la realización de un sistema neuronal artificial puede establecerse una estructura jerárquica similar. El elemento esencial de partida será la neurona artificial, que se organizará en capas; varias capas constituirán una red neuronal, y por último, una red neuronal (o conjunto de ellas), junto con las interfaces de entrada y salida, más los módulos convencionales adicionales necesarios, constituirán el sistema global de proceso. (Fig. 3).

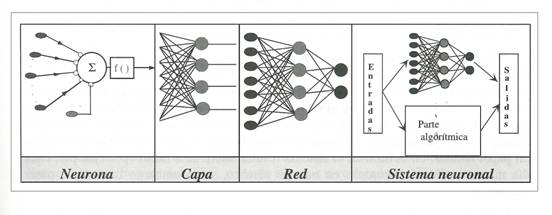
Figura 3. Estructura jerárquica de un sistema basado en ANS.

5. Modelo de una neurona artificial.

5.1. Modelo genérico de neurona artificial.

Como hemos comentado, una neurona es un procesador elemental tal que a partir de un vector de entrada procedente del exterior o de otras neuronas, proporciona una única respuesta o salida (Fig. 4).

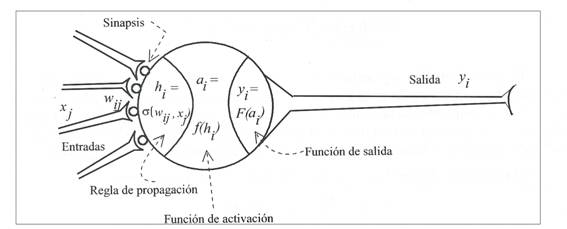
Figura 4. Modelo genérico de una neurona artificial.

Los elementos que constituyen dicha neurona son:

à Entradas: x(t). Las variables de entrada y salida pueden ser binarias (digitales) o continuas (analógicas) dependiendo del modelo de aplicación.

àPesos sinápticos: w. Representan la intensidad de interacción entre cada neurona presináptica j y la neurona postsináptica i.

àRegla de propagación: σ(w, x(t)). Proporciona el valor del potencial postsináptico, h(t), de la neurona i en función de sus pesos y entradas. Es decir

h (t) = σ(w, x(t))

La función más habitual es de tipo lineal, y se basa en una suma ponderada de las entradas con los pesos sinápticos

h(t) = = w

El peso sináptico w define en este caso la intensidad de interacción entre la neurona presináptica j y la postsináptica i. Dada una entrada positiva, si el peso es positivo tenderá a excitar a la neurona postsináptica, si el peso es negativo tenderá a inhibirla. Así, se habla de sinapsis excitadoras (peso positivo) e inhibidoras (peso negativo).

àFunción de activación o de transferencia: f. Proporciona el estado de activación actual, a, de la neurona i en función de su estado anterior, a, y de su potencial postsináptico actual. Es decir

En muchos modelos de ANS se considera que el estado actual de la neurona no depende de su estado anterior, sino únicamente del actual

La función de activación se suele considerar determinista, y en la mayor parte de los modelos es monótona creciente y continua. La forma de las funciones de activación más empleadas en los ANS se muestra en la siguiente tabla, donde representa el potencial postsináptico e el estado de activación.

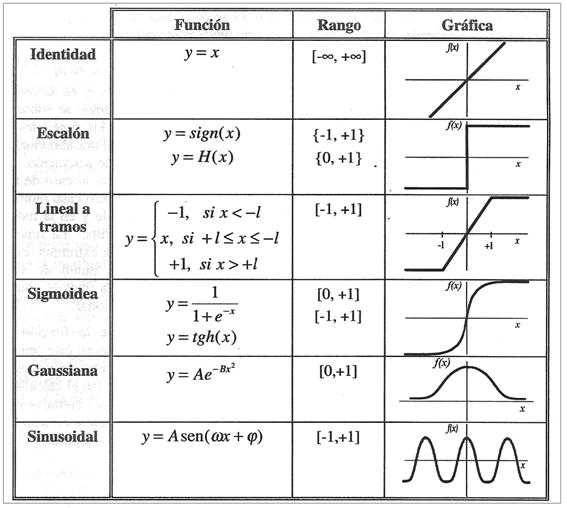
Figura 5. Funciones de activación habituales.

àFunción de salida: . Proporciona la salida actual, , de la neurona i en función de su estado de activación actual, . Muy frecuentemente la función de salida es simplemente la identidad , de modo que el estado de activación de la neurona se considera como la propia salida. Es decir

Por tanto, la operación de la neurona i puede expresarse de la siguiente forma:

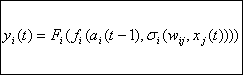
Por último, veamos como podría ser la interconexión entre varias neuronas:

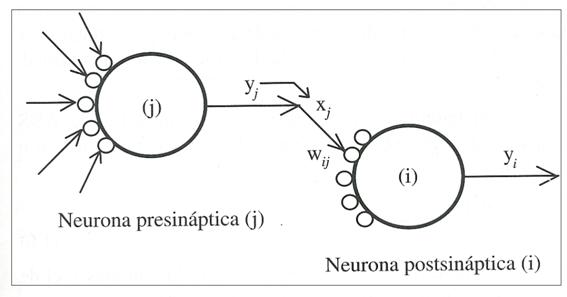
Figura 6. Interconexión entre una neurona

Presináptica y una neurona postsináptica.

5.2. Modelo estándar de neurona artificial.

Considerando que la regla de propagación es la suma ponderada y que la función de salida es la identidad, la neurona estándar consiste en:

àUn conjunto de entradas .

àUnos pesos sinápticos asociados a las entradas.

àUna regla de propagación . La más común suele ser .

àUna función de activación que representa simultaneamente la salida de la neurona y su estado de activación.

Todos estos elementos quedan recogidos en la siguiente ilustración que pone de manifiesto el modelo considerado.

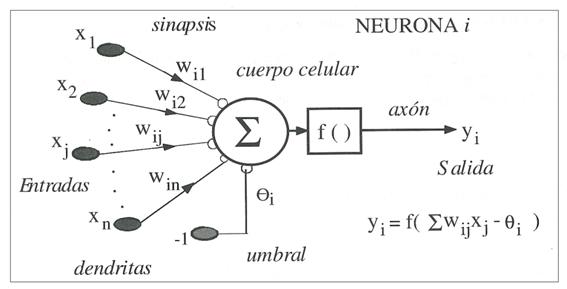
Figura 7. Modelo de neurona estándar.

Con frecuencia se añade al conjunto de pesos de la neurona un parámetro adicional, , que denominaremos umbral, que se resta del potencial postsináptico, por lo que el argumento de la función de activación queda

De forma equivalente, si hacemos que los índices i y j comiencen por 0 y definiendo y (constante) podemos obtener el comportamiento de la neurona a través de:

Tan sólo nos quedaría determinar que función de activación tendría la neurona para determinarla por completo. Dichas funciones son las mostradas en la tabla de la figura 5.

A continuación mostraremos algunos de los tipos más usuales de neuronas.

5.2.1. Dispositivos de umbral.

Consideraremos que las entradas son digitales, por ejemplo , y la función de activación es la escalón (Heavside), definida entre 0 y 1, se tiene

Como cuando , y cuando , se tiene

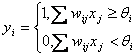
Es decir, si el potencial de membrana supera un valor umbral (umbral de disparo), entonces la neurona se activa, si no lo supera, la neurona no se activa. Este es el modelo de neurona del Perceptrón original o dispositivo de tipo umbral.

McCulloch y Pitts demostraron en 1943 que mediante redes basadas en este modelo de neurona se podía realizar cualquier función lógica.

5.2.2. Neurona sigmoidea.

Las entradas pueden ser tanto digitales como analógicas y las salidas exclusivamente analógicas. Tomando como función de activación una sigmoidea (Fig. 5), la cual se puede definir de las dos formas siguientes en función del intervalo considerado.

, con ]

Este es el modelo usado para el perceptrón multicapa.

6. Arquitectura de Redes Neuronales.

6.1. Definiciones Básicas.

Se denomina arquitectura a la topología o estructura en la que las distintas neuronas constituyentes de la red neuronal se asocian. En un ANS, los nodos se conectan por medio de sinapsis; esta estructura de conexiones sinápticas determina el comportamiento de la red. Las conexiones sinápticas son direccionales, es decir, la información sólo puede fluir en un sentido (desde la neurona presináptica a la neurona postsináptica).

En general, las neuronas se suelen agrupar en unidades estructurales denominadas capas. Dentro de una capa las neuronas pueden agruparse formando grupos neuronales. Dentro de una misma capa o agrupación, las neuronas suelen ser del mismo tipo. El conjunto de una o más capas constituye una red neurona.l.

Podemos distinguir tres tipos de capas: (Ver figura 14)

à Capa de entrada: compuesta por neuronas que reciben datos o señales procedentes del entorno.

à Capa de salida: aquella cuyas neuronas proporcionan la respuesta de la red neuronal.

à Capa oculta: aquella que no tiene una conexión directa con el entorno.

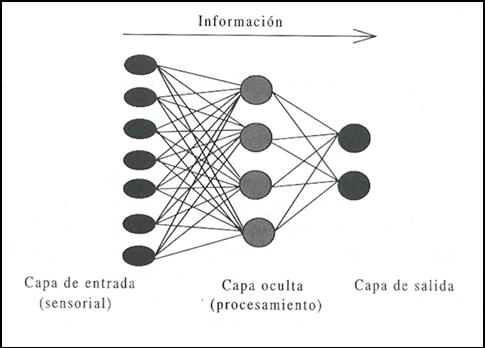
Figura 8. Capas de una red.

Las conexiones entre las enuronas pueden ser excitatorias o inhibidoras, según el signo del peso sináptico asociado a la conexión. Si dicho peso sináptico es negativo, entonces tendremos una conexión inhibitoria, si por el contrario éste es positivo estaremos frente a una conexión excitatoria. Esta distinción no suele usarse demasiado, ya que el peso y su magnitud vendrán determinados en cada instante por el algoritmo de entrenamiento.

Las conexiones pueden clasificarse también en conexiones intracapa y conexiones intercapa. Las primeras se corresponden con las conexiones entre las neuronas de una misma capa y, la segunda se corresponde a las conexiones entre neuronas de distintas capas.

6.2. Definición formal de Red Neuronal.

Para obtener una definición de red neuronal tenemos que hacer uso del concepto matemático de grafo. A través de este término, podemos definir una red neuronal de la siguiente forma:

Una red neuronal es un grafo dirigido con las siguientes propiedades:

1) A cada nodo i se le asocia un variable de estado .

2) A cada conexión (i, j) de los nodos i y j se el asocia un peso .

3) A cada nodo i se le asocia un umbral .

4) Para cada nodo i se define una función , que depende de los pesos de sus conexiones, del umbral y de los estados de los nodos j a él conectados. Esta función proporciona el nuevo estado del nodo.

6.3. Tipos de Redes Neuronales.

Una vez vistos los elementos básicos de toda red neuronal, se pasará a enumerar las diferentes estructuras en las que dichos elementos se pueden asociar.

6.3.1. Red Neuronal Monocapa.

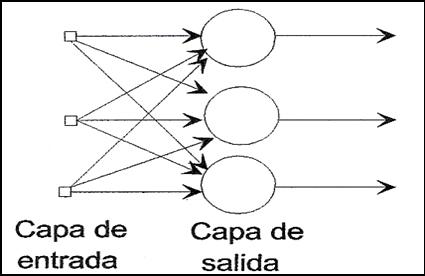
Se corresponde con la red neuronal más sencilla ya que se tiene una capa de neuronas que proyectan las entradas a una capa de neuronas de salida donde se realizan los diferentes cálculos. (Ver figura 9).

Figura 9. Red Neuronal Monocapa.

6.3.2. Red Neuronal Multicapa.

Es una generalización de la anterior, existiendo un conjunto de capas intermedias entre la capa de entrada y la de salida (capas ocultas). Este tipo de red puede estar total o parcialmente conectada. (Ver figura 10).

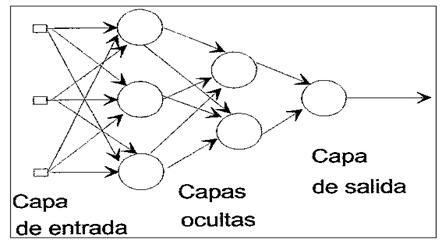
Figura 10. Red Neuronal Multicapa.

6.3.3. Red Neuronal Recurrente.

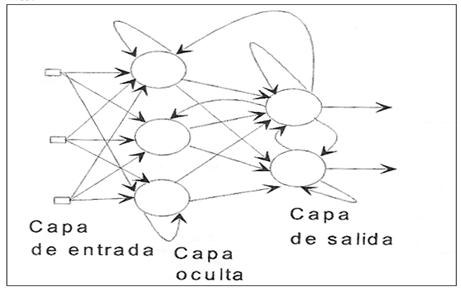
Este tipo de red se diferencia de las anteriores en la existencia de lazos de realimentación en la red. Estos lazos pueden ser entre neuronas de diferentes capas, neuronas de la misma capa o, entre una misma neurona. Esta estructura la hace especialmente adecuada para estudiar la dinámica de los sistemas no lineales. (Ver figura 11).

Figura 11. Red Neuronal Recurrente.

7. Modos de operación: Recuerdo y Aprendizaje.

7.1. Fase de APRENDIZAJE. Convergencia.

Puede definirse el aprendizaje como el proceso por el que se produce el ajuste de los parámetros libres de la red a partir de un proceso de estimulación por el entorno que rodea a la red. En la mayoría de los casos el aprendizaje consiste simplemente en determinar un conjunto de pesos sinápticos que permita a la red realizar correctamente el tipo de procesamiento deseado.

Al construir un sistema neuronal, se parte de un cierto modelo de neurona y de una determinada arquitectura de red, estableciéndose los pesos sinápticos iniciales como nulos o aleatorios. Para que la red resulte operativa es necesario entrenarla. El entrenamiento o aprendizaje se puede llevar a cabo a dos niveles:

1) A través del modelado de las sinápsis; que consiste en modificar los pesos sinápticos siguiendo una cierta regla de aprendizaje, construida normalmente a partir de la optimización de una función de error o coste, que mide la eficacia actual de la operación de la red.

Si denominamos al peso que conecta la neurona presináptica j con la postsináptica i en la iteración t, el algoritmo de aprendizaje, en función de las señales que en el instante t llegan procedentes del entorno, proporcionará el valor que da la modificación que se debe incorporar en dicho peso, el cual quedará actualizado de la forma:

El proceso de aprendizaje es usualmente iterativo, actualizándose los pesos de la manera anterior, una y otra vez, hasta que la red neuronal alcanza el rendimiento deseado.

2) A través de la creación o destrucción de neuronas; en el cual se lleva a cabo una modificación de la propia arquitectura de la red.

Los tipos de aprendizaje que pueden distinguirse son:

à Supervisado.

à No supervisado o Autoorganizado.

à Híbrido.

à Reforzado.

Los algoritmos de aprendizaje se basan usualmente en métodos numéricos iterativos que tratan de reducir una función de coste, lo que puede dar lugar a veces a problemas en la convergencia del algoritmo. En un sentido riguroso, la convergencia es una manera de comprobar si una determinada arquitectura, junto a su regla de aprendizaje, es capaz de resolver un determinado problema.

En el proceso de aprendizaje es importante distinguir entre el nivel de error alcanzado al final de la fase de aprendizaje para el conjunto de datos de entrenamiento, y el error que la red ya entrenada comete ante patrones no utilizados en el aprendizaje, lo cual mide la capacidad de generalización de la red. Interesa más una buena generalización que un error muy pequeño en el entrenamiento, pues ello indicará que la red ha capturado el mapping subyacente en los datos.

7.1.1. Aprendizaje SUPERVISADO.

En el aprendizaje supervisado se presenta a la red un conjunto de patrones, junto con la salida deseado u objetivo, e iterativamente ésta ajusta sus pesos hasta que la salida tiende a ser la deseada, utilizando para ello información detallada del error que se comete en cada paso. De este modo, la red es capaz de estimar relaciones entrada/salida sin necesidad de proponer una cierta forma funcional de partida. Es decir, si E[W] es una función que representa el error esperado de la operación de la red, expresado en función de sus pesos sinápticos W, se pretende estimar una cierta función multivariables a partir de muestras ( tomadas aleatoriamente por medio de la minimización iterativa de E[W] mediante aproximación estocástica (las técnicas de aproximación estocástica estiman valores esperados a partir de cantidades aleatorias observadas).

7.1.2. Aprendizaje NO SUPERVISADO o AUTOORGANIZADO.

El aprendizaje no supervisado se puede describir genéricamente como la estimación de la función densidad de probabilidad que describe la distribución de patrones (espacio de entrada).

En este tipo de aprendizaje se presentan a la red multitud de patrones sin adjuntar la respuesta que deseamos. La red, por medio de la regla de aprendizaje, estima , a partir de lo cual podemos reconocer regularidades en el conjunto de entradas, extraer rasgos o agrupar patrones según su similitud (clustering).

7.1.3. Aprendizaje HÍBRIDO.

En este caso existen en la red los dos tipos de aprendizaje básicos, supervisado y autoorganizado, normalmente en distintas capas de neuronas.

7.1.4. Aprendizaje REFORZADO.

Se sitúa a medio camino entre al aprendizaje supervisado y el autoorganizado. Como en el primero, se emplea información sobre el error cometido, pero en este caso existe una única señal de error, que representa un índice global del rendimiento de la red (solamente le indicamos lo bien o lo mal que está actuando). Como en el caso del no supervisado, no se suministra explícitamente la salida deseada.

7.2. Fase de RECUERDO o EJECUCIÓN. Estabilidad.

Una vez que el sistema ha sido entrenado, el aprendizaje se desconecta, por lo que los pesos y la estructura quedan fijos, estando la red neuronal ya dispuesta para procesar datos.

En las redes unidireccionales, ante un patrón de entrada, las neuronas responden proporcionando directamente la salida del sistema. Al no existir bucles de realimentación, no existe ningún problema en relación con su estabilidad. Por el contrario, las redes con realimentación son sistemas dinámicos no lineales, que requieren ciertas condiciones para que su respuesta acabe convergiendo a un estado estable o punto fijo. Existe una serie de teoremas generales que establecen las condiciones que aseguran la estabilidad de la respuesta en una amplia gama de redes neuronales en ciertas condiciones.

Para demostrar la estabilidad del sistema, dichos teoremas se basan en el método de Lyapunov. Dicho método constituye una manera asequible de estudiar la estabilidad de un sistema dinámico. Consiste en tratar de encontrar una función energía del sistema, que disminuya siempre en su operación, entonces el sistema es estable.

8. Clasificación de los modelos de redes neuronales artificiales.

Dependiendo del modelo de neurona concreto que se utilice, de la arquitectura o topología de conexión, y del algoritmo de aprendizaje, surgirán distintos modelos de redes neuronales.

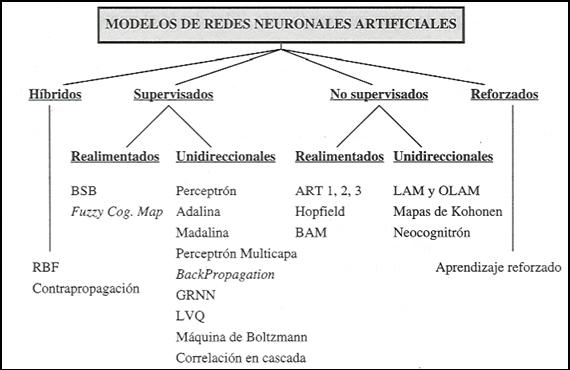
Figura 12. Clasificación de los ANS por el tipo de aprendizaje y la arquitectura.

9. El Perceptrón Simple (Rosenblatt, 1959).

Este modelo neuronal fue introducido por Rosenblatt a finales de los años cincuenta. La estructura del perceptrón se inspira en las primeras etapas de procesamiento de los sistemas sensoriales de los animales (por ejemplo, el de visión), en los cuales la información va atravesando sucesivas capas de neuronas, que realizan un procesamiento progresivamente de más alto nivel.

El perceptrón simple es un modelo neuronal unidireccional, compuesto por dos capas de neuronas, una de entrada y otra de salida (Figura 19). La operación de una red de este tipo, con n neuronas de entrada y m neuronas de salida, se puede expresar de la siguiente forma:

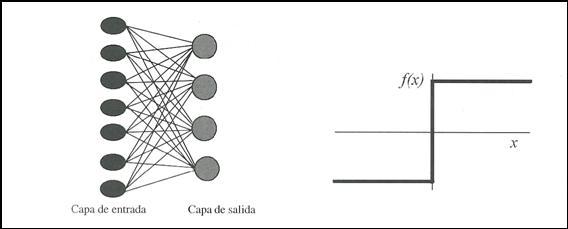
Figura 13. Perceptrón simple y función de transferencia de su neurona .

Las neuronas de entrada no realizan ningún cómputo, únicamente envían la información (en principio consideraremos señales discretas {0, 1}) a las neuronas de salida. La función de activación de las neuronas de la capa de salida es de tipo escalón (Ver Figura 5). Así, la operación de un perceptrón simple puede escribirse

con H(.) la función Heavside o escalón..

Por tanto, concluimos añadiendo que el perceptrón simple está formado por dispositivos de umbral y, por tanto, son útiles para la representación de funciones booleanas.

Ejemplo: Sea el perceptrón que se muestra en la figura 14, tal que su salida es

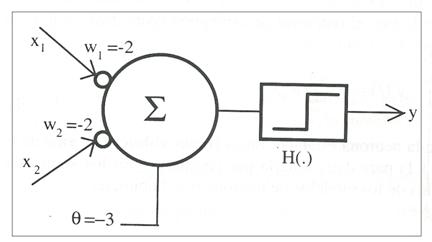
Figura 14. Perceptrón que implementa una puerta

lógica NAND de dos entradas.

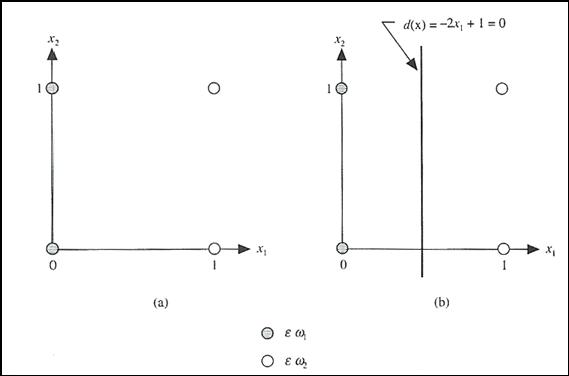
Las entradas y constituyen un plano, de tal forma que si lo representamos y marcamos los posibles valores de las entradas obtenemos el resultado mostrado en la ilustración 15.

Figura 15. A) Patrones que pertenecen a dos clases. B) Límite de decisión determinado por entrenamiento.

Dando valores lógicos a y podemos construir la siguiente tabla de verdad:


0	0	1
0	1	1
1	0	1
1	1	0

Podemos comprobar que se trata de la función lógica NAND.

NOTA: Puede demostrarse que un nodo de tipo umbral solamente puede implementar funciones linealmente separables, como la NAND. La XOR (OR-Exclusiva) no es linealmente separable, por lo que no puede ser implementada por un nodo sencillo como el anterior.

Ejemplo: Sea la red de dos capas con dos nodos en la capa de entrada, tal que las entradas son binarias. Desearíamos que la red fuera capaz de responder a las entradas de tal modo que la salida fuera la función XOR de las entradas. (Figura 16)

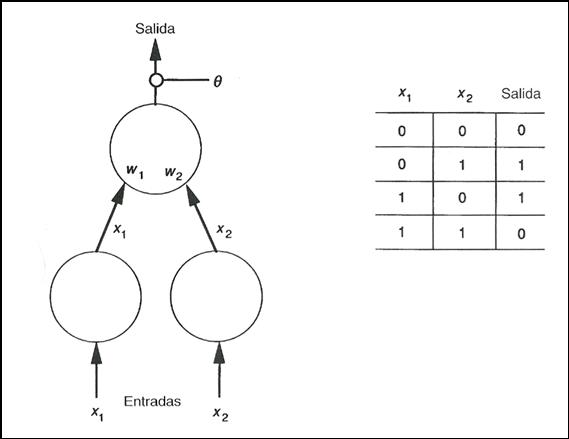
Figura 16. Perceptrón y tabla de comportamiento de la función lógica XOR.

Para ilustrar el funcionamiento de la función lógica XOR (OR-Exclusiva), veamos la siguiente tabla que pone de manifiesto su funcionalidad.


0	0	0
0	1	1
1	0	1
1	1	0

Nuevamente podemos ver como las entradas constituyen un plano en el que se pueden colocar los posibles valores de las entradas (Figura 17). De esta forma podemos observar que no hay forma de encontrar valores para , y tal que la representación de la salida de la red consiga separar el plano en dos regiones como máximo. Esto es para poder clasificar los puntos de una región como pertenecientes a la clase que posee una salida de 1, y los de otra región como pertenecientes a la clase que posee una salida nula. Esto se debe a que la sencilla unidad de umbral lineal no es capaz de llevar a cabo correctamente la función XOR.

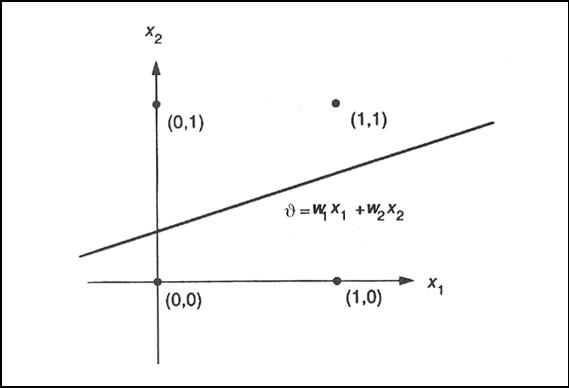
Figura 17. Plano con la solución alcanzada por el perceptrón anterior.

Para tratar de resolver esta dificultad tenemos que acudir al concepto de hiperplanos.

En el espacio tridimensional, un plano es un objeto de dos dimensiones. Un único plano puede descomponer el espacio tridimensional en dos regiones distintas; dos planos en tres o cuatro regiones distintas, dependiendo de sus orientaciones relativas, y así sucesivamente. Por extensión, en un espacio n-dimensional, los hiperplanos son objetos de (n-1) dimensiones.

Hay muchos problemas reales que implican la separación de regiones de puntos de un hiperplano en categorías individuales o clases, que deben distinguirse de otras clases. Una forma de hacer estas distinciones consiste en seleccionar hiperplanos que descompongan el espacio en regiones adecuadas. Esta tarea es bastante difícil de llevar a cabo en espacio de muchas dimensiones. Sin embargo, ciertas redes neuronales pueden aprender la descomposición adecuada, así que no es preciso determinarla por anticipado.

En un espacio general n-dimensional, la ecuación de un hiperplano se puede escribir de la forma

En donde los son constantes, con al menos un , y los son las coordenadas del espacio.

Continuando con el ejemplo de la XOR veamos como podemos encontrar una solución aproximada. Si observamos la figura 17 vemos que podríamos obtener una solución si descomponemos el espacio en tres regiones tal y como se pone de manifiesto en la figura 18. Una región pertenecería a una de las clases de salida, y las otras dos pertenecerían a la segunda clase de salida.

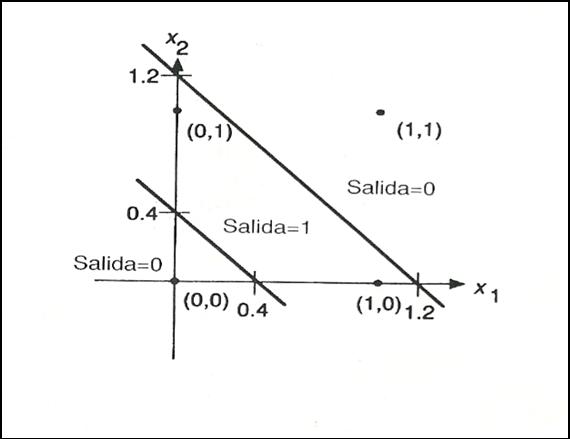
Figura 18. Solución que se desea alcanzar.

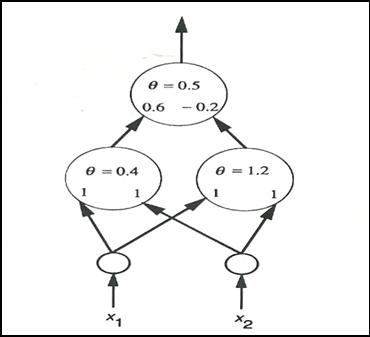
En la figura 19 podemos encontrar un dispositivo de umbral o perceptrón que lleva a cabo tal descomposición.

Figura 19. Perceptrón con el que se alcanza la solución deseada.

La adición de dos unidades de capa oculta, o capa intermedia, dan a la red la flexibilidad necesaria para resolver el problema. De hecho, la existencia de esta capa oculta nos da la capacidad de construir redes que puedan resolver problemas complejos.

ENTRENAMIENTO

1.- PARA QUE ENTRENAR

El objetivo que persigue el entrenamiento de una red neuronal es básicamente el de establecer unos valores para el vector de pesos con los cuales el error cometido al evaluar los ejemplos de entrenamiento sea mínimo.

Una vez calculados estos pesos la red estará lista para ser probada con otros patrones de test con los cuales no ha sido entrenada. El objetivo de esta nueva comprobación es que hemos de probar como se comporta la red cuando las entradas son distintas a las usadas para el entrenamiento.

Al entrenar una red neuronal con unos determinados ejemplos de entrenamiento e intentar minimizar el error a unas cuotas ínfimas, corremos el riesgo de especializar demasiado nuestra red, la cual se comportará de una manera optima con los ejemplos con los cuales ha sido entrenada, pero para ejemplos con los que no se ha entrenado se pueden producir errores considerables.

Todo esto nos lleva a la conclusión de que hay que minimizar el error, pero no hay que intentar rizar el rizo, ya que la especialización conlleva una pérdida de generalización.

Si este método de validación falla debemos optar por la opción de volver a entrenar la red desde el principio pero con unos pesos iniciales aleatorios distintos a los del entrenamiento anterior.

Si los resultados han sido correctos, nuestra red estará lista para funcionar y podremos asegurar que para nuevas entradas desconocidas para la red esta dará resultados mas o menos correctos.

Como última reseña hemos de indicar que aunque la fase de entrenamiento sea lenta y tediosa, una vez finalizada esta ya no hay que volver a entrenar, y además, como el calculo de los resultados que ofrece la red es lineal, estos se obtienen de una manera muy rápida. Todo esto nos hace llegar a la conclusión que las redes neuronales son una muy buena aproximación para el cálculo de funciones no computables algorítmicamente hablando como pueden ser los problemas con soluciones exponenciales, aunque por otro lado para problemas algorítmicamente computables se convierten en soluciones lentas y con unos resultados no tan exactos como fuera deseable.

2.- COMO ENTRENAR.

El entrenamiento de las redes neuronales se realiza mediante unos algoritmos de entrenamiento que se basan siempre en intentar buscar los pesos de las neuronas que ofrezcan mejores resultados.

En este trabajo vamos a centrarnos en uno solo de esos algoritmos, el algoritmo de BACKPROPAGATION.

Antes de comenzar a entrenar la red, lo primero que debemos hacer es definir la condición de parada. Esta condición puede ocurrir por varios motivos:

- Se ha alcanzado una cuota de error que consideramos suficientemente pequeña.

- Se ya llegado a un número máximo de iteraciones que hemos definido como tope para el entrenamiento.

- Se ha obtenido un error cero. Si mi red funciona a la perfección, ya no hay necesidad de tocar nada más

- Se ha llegado a un punto de saturación en el que por más que entrenemos ya no conseguimos reducir más el error.

3.- ENTRENAMIENTO DE UN PERCEPTRON.

Para comprender como se realiza el entrenamiento de una red de neuronas, lo primero que debemos de hacer es comprender el entrenamiento de una sola neurona, para luego acoplar varios entrenamientos individuales en uno colectivo para toda la red.

Para el entrenamiento de un perceptrón lo primero que debemos hacer es inicializar aleatoreamente su vector de pesos asociado, y después ir actualizando este para conseguir mejores resultados.

Para cada iteración del algoritmo se actualizará el vector de pesos:

De manera que:

Siendo h un parámetro al que denominaremos tasa de entrenamiento con un valor positivo y que hará la función de hacer que la convergencia sea más o menos rápida. Es recomendable que la tasa de entrenamiento sea pequeña ( entre 0.1 y 0.2) para que los resultados sean correctos.

Esta forma de recalcular los pesos se basa en el gradiente descendente de la función de error.

3.1.- FUNCIÓN DE ERROR

La función de error mide de una manera numérica la diferencia existente entre la salida ofrecida por la red y la salida correcta.

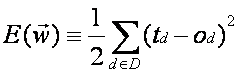
Se calcula de la siguiente manera:

Donde:

- D es el conjunto de ejemplos de entrenamiento.

- td es la salida correcta.

- od es la salida calculada por la red.

3.2.- GRADIENTE DESCENDENTE

El método del gradiente descendente se basa en buscar la dirección en la que una pequeña variación del vector de pesos hace que el error decrezca más rapidamente.

Para encontrar esta dirección usamos la que nos marca el gradiente de la función de error con respecto al vector de pesos.

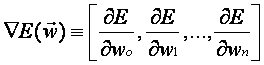
Para llegar a comprenderlo mejor veamos la siguiente figura en la que se representa el hiperplano resultante de la evaluación de una función de error dependiente de un vector de pesos bidimensional.

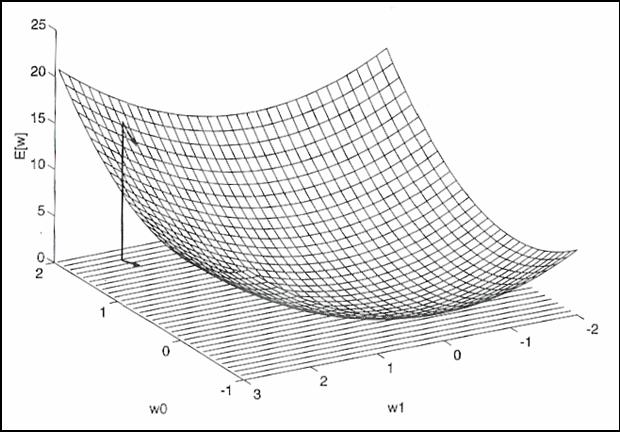
Figura 20. Hiperplano resultante de la evaluación de una función de error.

La flecha nos indica la dirección en la cual pequeñas variaciones en los pesos producen las mayores variaciones en la función de error, que es la misma dirección que la que indica el gradiente de la función de error con respecto del vector de pesos.

Así la actualización de los pesos para el método del gradiente descendente quedaría de la siguiente manera:

El algoritmo del gradiente descendente es el siguiente:

GRADIENTE_DESCENDENTE()

- Inicializar cada peso a un valor aleatorio.

- Repetir hasta que se cumpla la condición de terminación:

o Inicializar cada Dwi a cero.

o Para cada ejemplo de entrenamiento hacer:

§ Calcular la salida que ofrece la red

§

Para cada peso wi hacer:

o

Para cada peso wi hacer:

FIN GRADIENTE_DESCENDENTE

4.- ALGORITMO “BACKPROPAGATION”.

Cuando necesitamos representar problemas complejos, no nos basta únicamente con un simple perceptrón, sino que necesitamos una red de perceptrones interconectados entre ellos.

Para el entrenamiento de una red hemos de tener en cuenta que la salida de cada neurona no va a depender únicamente de las entradas del problema, sino que también depende de las salidas que ofrezcan el resto de las neuronas. Por este mismo motivo también podemos afirmar que el error cometido por una neurona no solo va a depender de que sus pesos sean los correctos o no, sino que dependerá del error que traiga acumulado del resto de neuronas que le precedan en la red.

Para controlar el error cometido hemos de redefinir la función de error, de tal forma que la nueva función de error es la siguiente:

Donde cada parámetro significa lo siguiente:

- es el vector de pesos.

- D es el conjunto de ejemplos de entrenamiento.

- d es un ejemplo de entrenamiento concreto.

- Salidas es el conjunto de neuronas de salida.

- k es una neurona de salida.

- tkd es la salida correcta que debería dar la neurona de salida k al aplicarle a la red el ejemplo de entrenamiento d.

- okd es la salida que calcula la neurona de salida k al aplicarle a la red el ejemplo de entrenamiento d.

Dentro de una red tenemos varios tipos de neuronas:

- Neuronas tipo n. Serán las neuronas de entrada a la red.

- Neuronas tipo h. Serán las neuronas internas de la red.

- Neuronas tipo n. Serán las neuronas de salida de la red.

Nótese que el número de neuronas de entrada a la red ha de ser igual al número de entradas del problema a resolver, y que es recomendable que el número de neuronas de salida sea igual al número de patrones distintos entre los que pretendamos clasificar los ejemplos de entrenamiento, así, un determinado ejemplo de entrenamiento pertenecerá al patrón que indique la neurona de salida cuya salida se aproxime más a una cota que nosotros definamos (por ejemplo: aquella cuya salida se aproxime más a 1).

Cuando haya varias neuronas con un valor de aproximación a la cota establecida que sea muy similar, podremos decir que “lo mas probable” es que la neurona sea de uno de esos patrones, sin embargo cuando solo haya una salida que se aproxime claramente más que el resto a la cota clasificaremos esa ejemplo dentro del patrón que indique esa neurona.

4.1.- PSEUDOCODIGO DEL ALGORITMO DE BACKPROPAGATION

Sea:

- ejemplos: conjunto de ejemplos de entrenamiento.

- h: tasa de entrenamiento.

- nin: número de neuronas de entrada de la red.

- nhidden: número de neuronas internas de la red.

- nout: número de neuronas de salida de la red.

Definimos:

RETROPROPAGATION(ejemplos, h, nin, nhidden, nout)

- Crear la red con el número de neuronas indicado (nin, nhidden, nout).

- Inicializar todos los pesos de todas las neuronas a un valor aleatorio.

- Hasta que se cumpla la condición de parada hacer:

o Propagar las entradas a través de la red y obtener las salidas.

o Propagar los errores de atrás hacia delante:

§ Para cada neurona de salida k calcular dk:

§

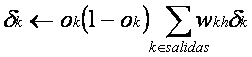
Para cada neurona intermedia h calcular dh:

§

Actualizar cada peso wji de la red:

·

con:

FIN RETROPROPAGATION

IMPLEMENTACIÓN

[ATRÁS]

1.\ PREFACIO.

Un ANS puede simularse mediantes programas ejecutados en ordenadores convencionales.Sin embargo, deberá realizarse en hardware si se desea aprovechar su capacidad de cálculo masivamente paralelo, permitiendo así su aplicación a problemas que deban tratarse cantidades masivas de datos. La tecnología de implementación más habitual hoy en día es la microelectrónica,VLSI,ULSI o WSI y la disponibilidad de potentes herramientas de CAD para diseño.

2.\ INTRODUCCIÓN.

Uno de los motivos más importantes del renacimiento de las redes neuronales en la década de los ochenta fue el desarrollo de la tecnología VLSI.Por una parte, posibilitó el desarrollo de computadores potentes y baratos,lo que facilitó la simulación de modelos de redes neuronales artificiales de un relativamente alto nivel de complejidad. Por otra parte, la integración VLSI posibilitó la realización hardware directa de ANS.

3.\ ALTERNATIVAS PARA LA REALIZACIÓN DE ANS.

a)Simulación software

Consiste en modelar el sistema neuronal mediante un programa, que puede ejecutarse en un ordenador secuencial convencional o bien sobre un computador de propósito general con capacidad de cálculo paralelo. Es la realización más usual y barata.

b)Emulación hardware

Se utilizan sistemas expresamente diseñados para emular un ANS, basados en CPU de altas prestaciones (RISC,DSP,...) o en otros microprocesadores diseñados específicamente para los ANS (aceleradores o neurocomputadores de propósito general).

c)Implementación hardware

Se trata de realizar físicamente la rede neuronal en hardware, mediante estructuras específicas que reflejan con cierta fidelidad la arquitectura de la red, que son denominadas neurocomputadores de propósito específico.La tecnología más habitualmente utilizada es la electrónica, bien utilizando dispositivos de lógica programable (como FPGA),bien mendiante integración microelectrónica, que da lugar a ASIC, denominados chip neuronales.

3.1.\SIMULACIÓN SOFTWARE DE ANS

Denominaremos simulación software de un ANS a su realización en forma de un programa ejecutable sobre un computador de propósito general.

Constituye siempre la primera etapa en el desarrollo de un ANS, por ser el procedimiento más simple, rápido y económico.

El proceso de simulación de ANS comienza mendiate el modelado mendiante programas de ordenador escritos en lenguajes de alto nivel como C o PASCAL, aunque de esta manera se pierde la capacidad de cáculo en paralelo.

Los principales problemas de la simulación en computadores convencionales surgen del carácter esencialmente secuencial de éstos, en contrapartida al inherente paralelismo de los ANS.

Por ejemplo, un problema que precise una red de 100 neuronas (lo que constituye un sistema relativamente pequeño), incluiría del orden de 10000 conexiones o pesos sinápticos.Si suponemos que un microprocesador realiza alrededor de 10 millones de multiplicaciones y acumulaciones por segundo, podría ejecutar aproximadamente 1000 fases de recuerdo por segundo.

Si el tiempo de respuesta necesario es del orden de milisegundo, la simulación en un ordenador convencional resultará sufuciente.

Sin embargo, si la aplicación requiere 300 neuronas, la red contendrá 90000 conexiones, con lo que sólo podrá realizar 100 fases de recuerdo por segundo.Así para un problema cuya resolución precise miles o millones de neuronas, como puede ser una tarea de visión o un tratamiento de imágenes (256x256 pixeles, cada pixel representa una neurona),la simulación sobre un ordenador convencional puede resultar inoperante y se hace necesaria una solución distinta, en la que el paralelismo de cálculo sea manifiesto.Una solución puede ser la utilización de máquinas vectoriales o paralelas de propósito general, el inconveniente es su precio y la no fácil accesibilidad.

3.2.\ EMULACIÓN HARDWARE DE ANS

Con el término emulación hardware nos referimos a la utilización de una estructura de procesamiento con cierta capacida de cálculo paralelo, especialmente diseñada para el trabajo con ANS.

Se trata ésta de una solución intermedia entre la simulación y la verdadera realización hardware.Normalmente se trata de utilizar una tarjeta coprocesadora dependiente de un cierto host construida tomando com base microprocesadores de altas prestaciones(RISC,DSP,..) o a chips neuronales.Mediante un software de simulación adecuado, se pueden aprovechar las características de cálculo limitadamente paralelo de la tarjeta utlizada para acelerar la simulación de un ANS,por lo que se denominan aceleradores.

No suelen resultar económicas y tampoco se aprovechan totalmente las posibilidades de cálculo paralelo de la red.

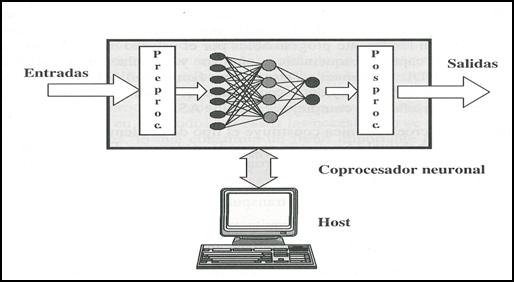
Figura 21. Estructura host-coprocesador neuronal, constituyendo un neurocomputador.

3.3.\ REALIZACIÓN HARDWARE DE ANS

Consiste en construir físicamente un sistema cuya arquitectura refleje en cierta medida la estructura de la red neuronal.Debido a ello, el sistema hardware debe soportar un gran número de conexiones, en ocasiones globales, y un flujo elevado de comunicaciones de datos.Estas cirscuntancias limitan considerablemente el tamaño de la red neuronal que puede ser implementada.

Este tipo de realización está especialmente indicado para aplicaciones especiales donde se precisa un alto rendimiento, ya que el diseño se realiza para un cierto modelo de red neuronal y para una aplicación concreta.

Son las tecnologías electrónicas las más empleadas en la actualidad, pese a no ser las más idóneas(especialmente en cuanto a conectividad).

Las razones fundamentales son la amplia disponibilidad de los procesos tecnológicos microelectrónicos y el elevado grado de automatización del diseño.

La realización electrónica se lleva a cabo mendiante tecnologías microelectrónicas, en forma de ASIC(Application Specific Integrated Circuit), o mediante FPGA (Field Programmable Gate Arrays). Aunque el diseño de ASIC es lo más habitual, en la actualidad la realización mendiante FPGA presenta la ventaja de un periodo de desarrollo más corto. Aunque su densidad de puertas es menor, son facílmente programables por el usuario mendiante herramientas de CAD que permiten captura esquemática, síntesis y simulación a partir de una descripción en un HDL (Hardware Description Language), por ejemplo, VHDL o VERILOG. Las FPGA resultan interesantes para el desarrollo rápido y económico de prototipos o series pequeñas, aunque no permiten diseños tan complejos como los ASIC.

Sin duda, la microelectrónica costituye el tipo de implementación hardware de redes neuronales más habitual.Su diseño se puede structurar de forma jerárquica de modo que la realización de un sistema neuronal puede llevarse a cabo desde distintos niveles de abstracción:

* Nivel de sistema: Utilización de coprocesadores,DSP,..

* Nivel de estructura funcional: ALU's específicas.

* Nivel de puerta lógica: Lógica de pulsos,lógica estocástica.

* Nivel de puerta analógica: Redes de Hopfield,Kohonen,Maxnet,...

*Nivel de transistor: Realización de chips de muy alta densidad de integración y elevado número de neuronas, como redes de Hopfield.

* Nivel de modelo: Distintos modelos de los transistores CMOS.

* Nivel de layout.

* Nivel de procesos: Modificadores del proceso CMOS (EEPROM,fusibles)

4.\ ESPECIFICACIONES DE UN NEUROCOMPUTADOR

Por neurocomputador entendemos un dispositivo con capacidad de cálculo paralelo, diseñado para la emulación de redes neuronales artificiales, y en el que cada una de sus unidades procesadoras puede representar una neurona o más. Habitualmente se trata de placas coprocesadoras o aceleradoras, construidas a partir de microprocesadores convencionales o neurochips, que dependen de un host. El papel del host (un computador convencional) es el de proporcionar al usuario un medio de comunicación con la placa procesadora mediante su teclado, pantalla y unidades de almacenamiento masivo. Además, el host gestiona el sistema completo por medio de un proggrama que actúa sobre la tarjeta coprocesadora.

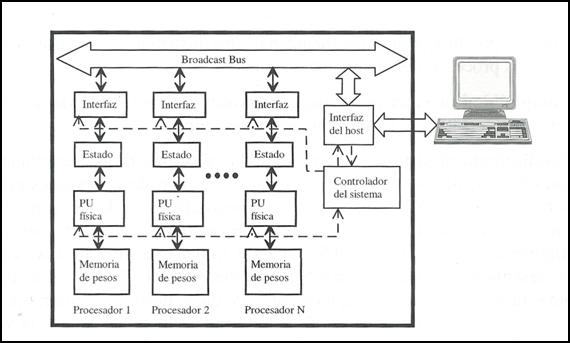
Figura 22. Neurocomputador de propósito general.

Arquitectura clásica orientada a bus, compuesta por un conjunto de unidades procesadoras o PU, dotadas de memoria local para el almacenamiento de los pesos de las neuronas virtuales que emulan, y conectadas a un bus local que las comunica con el host.

Aspectos relevantes:

· Grado de programabilidad del sistema.(flexibilidad) Indica la versatilidad para la emulación de diferentes modelos neuronales.

· Número de unidades de procesamiento.(paralelismo) Indica el paralelismo del neurocomputador(disponer de un procesador por neurona suele resultar costoso, por lo que habitualmente hay que distribuir las neuronas a emular entre los procesadores realmente disponibles).

· Complejidad de cada procesadr individual. Es un ímdice de la potencia de cálculo de cada unidad procesadora.

· Rendimiento del sistema. Mide la velocidad de procesamiento

4.1\ NEUROCOMPUTADORES DE PROPÓSITO GENERAL

Son los diseñados para emular un gran número de modelos de redes neuronales; constituyen por tanto máquinas flexibles y versátiles.Tienen un alto grado de programabilidad y sus unidades procesadoras o PU serán más complejas(son un número no muy elevado por lo que cada unidad deberá emular más de una neurona).

4.2\ NEUROCOMPUTADORES DE PRÓPOSITO ESPECÍFICO

Se trata de sistemas limitados a la emulación de un único modelo neuronal. Optimizan la ocupación de área de silicio y alcanzan mayores velocidades de procesamiento para ese modelo concreto. Como contrapartida, son menos flexibles y limitadamente programables. Están constituidos por unidades de procesado o PU más simples, pero menos flexibles, aunque podrá incluir un número mayor de ellas.Dentro de esta categoría estarían incluídos los desarrollados en torno a chips neuronales de propósito específico.

5.\ ASPECTOS GENERALES DE LA REALIZACIÓN VLSI

El aumento continuo de la densidad de integración hace que la tecnología VLSI se adapte muy bien a la implementación de sistemas paralelos, como es el caso de los neurocomputadores.Algunos de los mayores problemas de diseño a la hora de implementar estos sistemas (analógicos o digitales) en silicio son los siguientes:

- Los modelos neuronales requieren de altos niveles de conectividad.

- Se requiere alta velocidad de procesamiento y de comunicación de datos.

- Debe optimizarse la representación de los datos y el almacenamiento de los pesos.

El diseño de neurocomputadores que optimicen paralelismo de cómputo, rendimiento y flexibilidad precisa tener en cuenta las siguientes circunstancias que se dan en la integración VLSI.

- La complejidad de los diseños favorece el desarrollo de estructuras simples, regulares y rplicables.

- El cableado ocupa gran parte del espacio eu un circuito integrado.

- Los retrasos en las comunicaciones degradan el rendimiento.

- Las tecnologías MOS,de bajo consumo,requieren concurrencia para lograr muy altos rendimientos.

- Debe haber una perfecta coordinación entre la entrada/salida con los cálculos internos, de modo que el sistema no vea limitado su rendimiento a causa de una entrada salida lenta.

Teniendo en cuenta las anteriores circunstancias, un buen diseño VLSI de un neurocomputador debería incluir las siguientes propiedades arquitecturales:

- Simplicidad en el diseño, que debe onducir a una arquitectura basada en reproducciones de unas pocas celdas simples.

- Modularidad que limite los requerimientos de comunicaciones, reduciendo el coste en conexiones.

- Diseño expandible y escalable.

En la actualidad existen realizaciones de hasta algunos cientos de neuronas incluyendo miles de sinapsis por unindad de procesado (haciendo uso de tecnologías analógicas).

5.1\ ARQUITECTURAS RECONFIGURABLES

Mención aparte merecen las realizaciones digitales de neuroemuladores basadas en la aplicación de dispositivos con la capacidad de modificar sus estructuras hardware, adaptándola a los requisitos de la aplicación a la que se desea realizar.

Perteneciente a la misma familia de dispositivos que las PLD's,PROM, PAL o EPLD, las FPGA's (Field Programmable Gate Array) son dispositivos programables de elevado número de puertas, constituidos por una matriz de celdas lógicas o CLB (Configurable Logic Block) altamente interconectables a través de una malla de conexiones.Cada una de estas celdas contiene tanto lógica combinacional como biestables proporcionando así capacidad para generar lógica secuencial.El interés que presentan estos circuitos lógicos reside en la posibilidad de configurarlos adecuándolos a los requisitos de los usuarios. Debido al elevado número de puertas integradas en un dispositovo de este tipo, y a su reducido coste económico y de tiempo de desarrollo, podemos encontrar gran cantidad de aplicaciones en las que las FPGA's cumplen un papel importante.

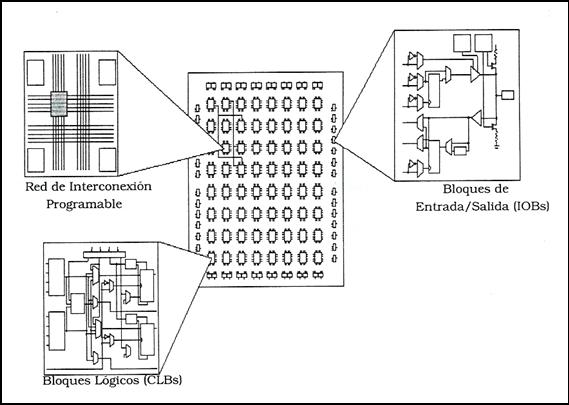
Figura 23. FPGA de Xilinx.

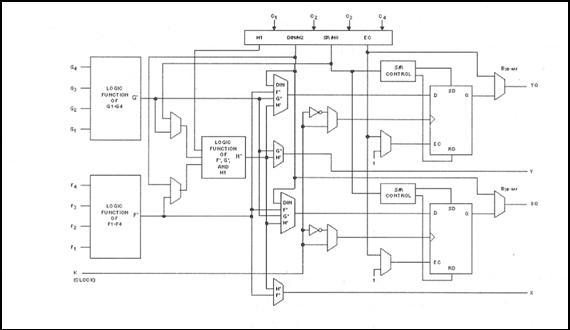
Figura 24. Estructura básica de un CLB de FPGA de la compañía Xilinx.

6.\ IMPLEMENTACIÓN ANALÓGICA vs DIGITAL

6.1\ PROS Y CONTRAS DE LA REALIZACIÓN ANALÓGICA

Una neurona puede implementarse fácilmente mediante dispositivos analógicos, tratando de aprovechar las leyes físicas para la realización de cálculos. Así, la suma ponderada de la neurona surge de manera directa de la aplicación de las leyes de Kirchhoff en forma de sumas de corrientes. Además, las características no lineales de los dispositivos favorecen le realización de funciones de activación de tipos sigmoideo.

Por tanto, inicialmente la realización analógia parece presentar importantes ventajas.

Un posible esquema de una neurona analógica se muestra en la figura, donde el soma se representa mendiante un amplificador operacional (triángulos), y los pesos sinápticos mediante resistencias.

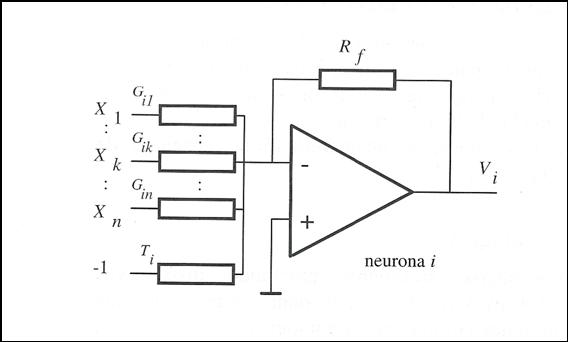
Figura 25. Modelo sencillo de neurona analógica basada en un amplificador operacional.

Este circuito presenta notables limitaciones como la de operar con una única función de activación ,excesivo consumo de potencia y la gran cantidad de área ocupada por el dispositivo y su red de resistencias, que no son reajustables.

Los circuitos analógicos, en general, presentan la interesante característica de permitr el procesamiento de mas de 1 bit por transistor, así como proporcionar una velocidad de proceso mayor que la de los circuitos digitales.

Aunque este tipo de implementación sea muy adecuada para la realización de modelos de redes neuronales cabe comentar algunos aspectos negativos de dicha realización:

- Comparándolos con los circuitos digitales, los analógicos son más susceptibles al ruido en la señal, ruido cruzado,efectos térmicos, variaciones en la tensión de alimetación,....

- La precisión proporcionada por el procesamiento analógico está limitada normalmente a 8 bits, lo que resulta inadmisible para muchos algoritmos de aprendizaje (como el BackPropagation).

- El mayor problema atribuible a la integración analógica la no escalabilidad con la tecnología.

6.2\ PROS Y CONTRAS DE LA REALIZACIÓN DIGITAL

La realización digital de redes neuronales se basa en el almacenamiento de los pesos y activaciones neuronales en registros, y en la utilización de estructuras de cálculo clásicas(multiplicadores,AL's,...).

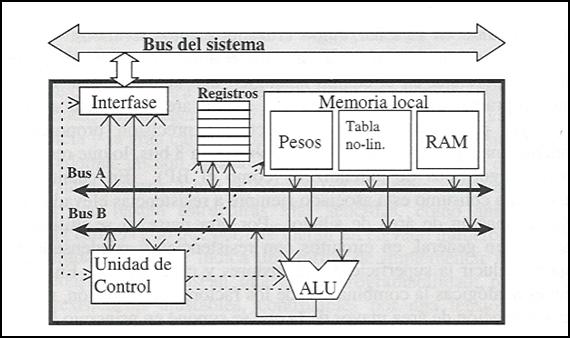
Figura 26. Unidad de procesamiento digital genérica que implementa un conjunto de neuronas virtuales.

Para las redes neuronales menos inspiradas en la biología, es decir,casi todos los modelos convencionles de ANS(MLP,SOFM,RBF,...) la integración digtal en un neurochip proporciona características muy interesantes, como flexibilidad en el diseño, posibilidad de integrar la fase de aprendizaje, realización de diseños expandibles y precisión elevada.Los diseños digitales proporciona mayores ventajas globales, pues hay que tener en cuenta que rango dinámico y precisión son aspectos críticos en muchos modelos neuronales (como el BackPropagation), y con la tecnología digital es posible alcanzar el nivel requerido.

Con todo, una de las grandes ventajas del diseño de circuitos digitales VLSI es la disponibilidad de potentes paquetes CAD, y la posibilidad de abordar los diseños con una metodoloía modular. Además, otra importante ventaja es la rápida adecuación de los diseños digitales a las nuevas tecnologías disponibles con mayor nivel de integración (escaabilidad con la tecnología), junto con la disponibilidad actual de herramientas de síntesis automática a partir de descripciones en algún lenguaje de descripción de hardware (como pueden ser VHDL o VERILOG ) del circuito a construir, diminuyendo notablemente los tiempos de desarrollo y abaratando costes.

Obviamente, las desventajas de la implementación digital son el gran consumo de área de silicio y la velocidad de ejecución relativamente lenta (en comparación con las realizacione analógicas).

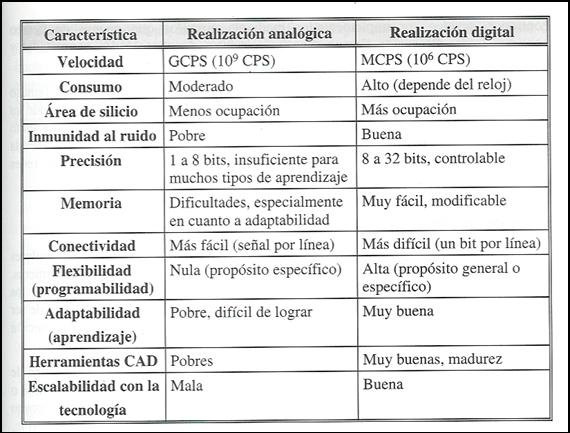
Figura 27. Realización análogica frente a digital.

APLICACIONES

[ATRÁS]

INTRODUCCIÓN

A continuación pasamos a estudiar varios problemas de ejemplo resueltos utilizando redes neuronales. Para el estudio de estos problemas nos hemos basado en diversa documentación ya que no existía un documento preciso que resolviera con exactitud la totalidad de los problemas.

Estudiaremos los siguientes problema:

1.- RECONOCIMIENTO DE ROSTROS MEDIANTE UNA

ARQUITECTURA BASADA EN REDES NEURINALES.

2.- RECONOCIMIENTO DE FIRMAS USANDO UNA

ARQUITECTURA DE REDES MULTICAPA.

3.- RECONOCIMIENTO DE PATRONES A PARTIR DE IMÁGENES

AÉREAS.

Para cada uno de estos problemas discutiremos la arquitectura propuesta, el funcionamiento básico del sistema y los resultados obtenidos a partir de experimentos realizados.

Al final expondremos diversa bibliografía donde es posible obtener una más amplia información del problema.

1.- RECONOCIMIENTO DE ROSTROS MEDIANTE UNA ARQUITECTURA BASADA EN REDES NEURONALES

Las redes neuronales son una herramienta matemática que permite la solución de una gran variedad de problemas, en particular aquellos de difícil modelado. En este trabajo se presenta una arquitectura basada en redes neuronales para la identificación de rostros. La arquitectura está formada de varios clasificadores cada uno compuesto, a la vez, de una red neuronal estándar tipo ART2 conectada a un Mapa de Memoria (MM). Las salidas de los diferentes clasificadores están conectadas a un sumador común (registro de evidencias) y a un conjunto de comparadores permitiendo la fusión de datos. Se prueba el desempeño de la arquitectura con un conjunto limitado de diez rostros.

1.1-Introducción

El rostro humano es un patrón muy complejo. Los humanos detectamos e identificamos

rostros en una imagen con muy poco esfuerzo. El reconocimiento automático de tales

patrones es, a la vez, un problema difícil e interesante. En años recientes este problema

ha atraído la atención de muchos científicos.

Un sistema para localizar e identificar correctamente rostros humanos sería útil en muchas aplicaciones tales como la identificación de criminales y en sistemas de seguridad y autentificación. Otras aplicaciones donde el reconocimiento de patrones puede ser usado incluyen la asistencia en el reconocimiento del habla y la comunicación visual a través del teléfono y otros medios.

Un sistema completo para el reconocimiento de rostros humanos debería permitir

realizar las siguientes tareas:

1. Determinar si una imagen contiene un rostro. Si es así, determinar su número,

posición y tamaño.

2. Determinar la identidad de cada rostro.

3. Proporcionar una descripción acerca del rostro (felicidad, enojo, tristeza, etcétera), y

4. Entregar información extra, por ejemplo, edad, sexo, etcétera.

Obviamente esta tarea es bastante compleja, siendo aún un problema difícil de

resolver. Muchos aspectos acerca del reconocimiento de rostros quedan por ser resueltos.

Varios métodos para el reconocimiento de rostros humanos han sido propuestos, por

ejemplo, otros métodos basados en redes neuronales, los métodos

usando imágenes de mosaico, y los métodos usando eigen-caras.

En este artículo nos concentraremos en dar solución al punto 2 de la problemática

arriba descrita suponiendo que el rostro ha sido localizado, esto es, el punto 1 ha sido

resuelto. Para esto se propone el uso de una nueva arquitectura compuesta de varios

clasificadores. Una arquitectura similar, compuesta de un solo clasificador, es usada en

el libro de Rayón y Figueroa (ver referencias) para el reconocimiento de formas poligonales simples. El funcionamiento de la nueva arquitectura se basa en el hecho de que para reconocer un rostro es necesario descomponerlo en un conjunto de partes llamadas características visuales (CV). Una CV pudiera ser, por ejemplo, una región alrededor de un punto, un conjunto de puntos, etcétera. A partir de cada CV, un vector de atributos es obtenido. Este vector de atributos es entonces usado para entrenar la red neuronal y construir su mapa de memoria con el clasificador correspondiente.

Durante la etapa de reconocimiento, una lista restringida de las personas obedeciendo

a una descripción de entrada es obtenida en una primera instancia, a la salida del

registro de evidencias, en forma de un histograma. Finalmente, esta lista se reduce a

través de un método de recorte (el conjunto de comparadores hace esto) para obtener

la lista final de posibles candidatos correspondiendo a la descripción de la imagen de

prueba.

1.2.-Arquitectura y funcionamiento.

Como mencionamos anteriormente, la arquitectura propuesta para el reconocimiento de

rostros humanos se compone de varios clasificadores, cada uno compuesto, a la vez,

de una red neuronal (RN) estándar tipo ART2 conectada a un Mapa de Memoria

(MM). Las salidas de los diferentes clasificadores están conectadas a un sumador

(registro de evidencias) común y a un conjunto de comparadores (figura 1). Para ser

útil, la arquitectura necesita que cada RN sea entrenada y que cada mapa de memoria

sea construido. Para esto usamos la siguiente metodología la cual está dividida en dos

fases, de inicialización y de indexado (figura 2). Es durante la primera fase que la RN es

entrenada y el MM es construido. Nótese que ambas fases comparten dos etapas:

detección de características visuales y codificación de características visuales.

El acrónimo ART viene del inglés Adaptive Resonance Theory, modelo inicialmente propuesto por G. A. Carpenter and S. Grossberg en 1986 para extender de los mecanismos de aprendizaje competitivos de contrapropagación y mapas autoorganizados (ver referencias). El 2 de ART 2 indica que la red puede procesar entradas analógicas, a diferencia de la ART 1, que solo es capaz de procesar entradas binarias.

Así pues, la arquitectura quedaría:

Figura 28. Arquitectura propuesta

Dónde cada red neuronal ART2 está conectada a un mapa de memoria cuyas salidas son entradas de sumadores conectados finalmente a una etapa de comparadores.

El funcionamiento de la arquitectura propuesta se basa en el hecho de que para reconocer un rostro, es necesario descomponerlo en un conjunto de partes llamadas características visuales (CVs). Estas CVs permitirán como veremos más adelante, el reconocimiento eficiente de personas a través de información visual.

Para detectar las características visuales precedemos:

Un conjunto selecto de puntos es primeramente detectado de una imagen del rostro.

Estos puntos son los mostrados en la figura mostrada a continuación. Actualmente, estos puntos son seleccionados manualmente. A partir de estos cinco puntos, otros cuatro puntos son calculados y marcados. Todos estos puntos serán llamados en adelante puntos de interés. Se muestran a continuación y son obtenidos en términos de la distancia entre los puntos 2 y 3. Con este conjunto de puntos, la siguientes CVs son derivadas:

a. Todos los píxeles encerrados en el rectángulo formado por los puntos 6,7, 8 y 9.

b. El triángulo formado por los puntos 1, 2 y 5.

c. El triángulo formado por los puntos 2, 3 y 5.

d. El triángulo formado por los puntos 3, 4 y 5.

e. El triángulo formado por los puntos 1, 4 y 5.

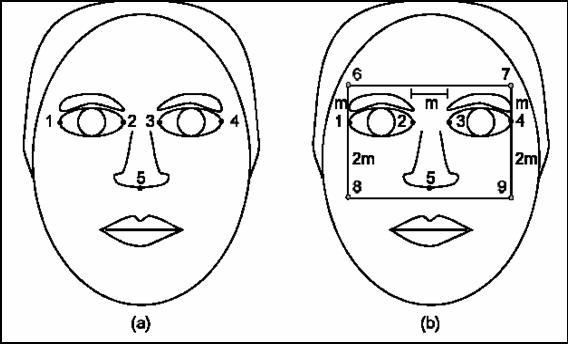
Figura 29. Obtención de CVs

Las fases de la metodología llevada a cabo, es decir: Inicialización e indexado se pueden resumir con la siguiente figura:

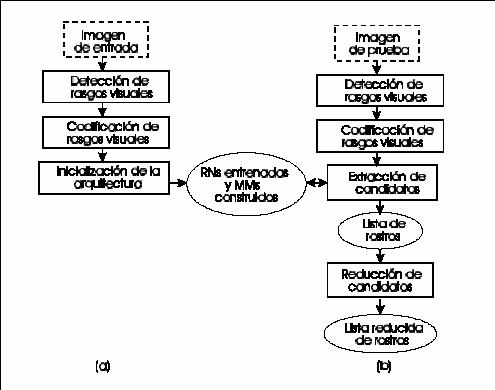
Figura 30.

(a) à Fase de Inicialización. (b) à Fase de indexado.

Las características visuales obtenidas en anteriormente son codificadas en términos de vectores de atributos; para calcular estos vectores se procede:

a.-Los cinco puntos 1, 2, 3, 4 y 5 mostrados anteriormente son codificados mediante el siguiente vector de tres componentes:

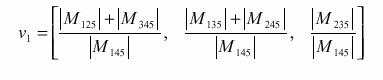
Dónde:

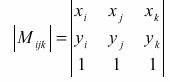
b.-Los niveles de intensidad encerrados por la ventana formada por los píxeles 6,

7, 8 y 9 son codificados en forma global como un vector de atributos compuesto por tres de los invariantes a translación, rotación y escala de (ver referencias: M. K. Hu) Experimentalmente, hemos probado que de entre los siete invariantes, los propuestos son los menos sensibles a cambios. Sea este vector:

Estos dos vectores de atributos (a los que alguna de las referencias denominan VA) son usados para entrenar las redes neuronales.

A continuación mostramos la detección de cada uno de los puntos de interés en una fotografía con rostro real:

Figura 31. Puntos de interés en una fotografía real.

1.3.- Inicialización.

Para llevar a cabo esta fase, un procedimiento compuesto de tres etapas es usado.

Cada una de estas etapas es explicada con detalle a continuación.

Etapa de entrenamiento de la red neuronal y construcción del MM:

Durante esta etapa, cada ART2 y su MM son, respectivamente, entrenada y construido.

Para esto el siguiente procedimiento es aplicado:

Al final de este procedimiento iterativo, la arquitectura habrá sido inicializada, esto es

las RNs y sus MMs habrán sido, respectivamente entrenadas y construidos.

La arquitectura final tiene la misma estructura que la mostrada en la figura 1, excepto

que el número de clasificadores es dos, uno por cada vector de atributos obtenido.

Nótese que cada ART2 tiene como entrada un vector de atributos y un número de

salidas igual al número de clases generadas por la ART2, dependiendo del factor de

vigilancia usado (ver referencias). Nótese también que cada MM tiene tantas filas como salidas provistas por la ART2 y tantas columnas como rostros usados para entrenar la ART2. Cada localidad del MM contiene un valor el cual representa el número de veces que un VA se encuentra presente en cada rostro entrenado. Este valor es ponderado

dependiendo del número de objetos conteniendo ese VA, entre más objetos contengan

ese VA, más pequeño será el peso asignado a ese VA.

El conjunto de compuertas de habilitación determina el modo de operación del sistema

(inicialización o indexado). El registro de evidencia almacena los votos ponderados

obtenidos por cada rostro durante la etapa de selección de candidatos.

Finalmente, el conjunto de comparadores es usado durante la etapa de reducción de

candidatos para seleccionar de entre estos rostros, aquellos con más

votos en términos de un umbral previamente escogido. Normalmente cualquiera de

estos rostros corresponderá al rostro presente en la imagen de prueba. Idealmente, la

lista reducida debería contener el modelo del rostro presente en la imagen.

Una red neuronal ART2 fue escogida ya que permite, por un lado, agrupar

automáticamente patrones para formar cúmulos de una manera auto organizada y, por

otro lado, debido a sus propiedades inherentes de indexado. Cada MM es construido conforme cada red es entrenada.

Selección del umbral (¶) de vigilancia para cada clasificador:

Recuérdese que elnúmero de cúmulos provistos por una ART2 depende del valor escogido para ¶

Si el valor escogido para ¶ es muy pequeño, una gran cantidad de cúmulos será generada (vectores de atributos muy similares serán puestos en cúmulos diferentes).

Inversamente, si el valor escogido para ¶ es muy grande, pocos cúmulos serán

generados (vectores de rasgos muy disimilares serán agrupados en el mismo cúmulo).

En este trabajo, el ¶ para un clasificador dado fue escogido de forma que el clasificador

permitiera diferenciar lo mejor posible entre VAs de personas diferentes y agrupar VAs

de la misma persona. Para lograr esto, se calculó, primeramente, la diferencia E entre

VAs de personas diferentes y la diferencia F entre VAs de la misma persona se

seleccionó un valor de umbral inicial ¶0, como el promedio de E. Enseguida, se

comparan los valores de E y F con el valor de ¶0. Si E > ¶0, significa que ¶0 diferenció

los VAs de personas diferentes, y se incrementa en 1 un contador CD (previamente

inicializado a cero). Si F > ¶0, significa que ¶0 confunde los VAs de la misma persona, y se incrementa en 1 un contador CC (previamente inicializado a cero).

Este mismo proceso se repitió para diferentes valores de i con i=i-1+. Finalmente, se seleccionó el valor de umbral óptimo como el máximo de CD-CC, esto es aquel que diferencia mejor entre VAs de personas diferentes y confunde menos entre VAs de la misma persona.

Ponderación de los mapas de memoria:

Una vez que los mapas de memoria han sido construidos, estos son ponderados. Para esto se usa el siguiente procedimiento

donde Mj[l,i] es una de las localidades del j-ésimo mapa de memoria, Cj el número de

cúmulos generado por el j-ésimo clasificador y nol el número de objetos conteniendo el

l-ésimo vector de atributos.

1.4- Indexado.

Durante esta fase, los vectores de atributos calculados a partir de las características

visuales en una imagen de prueba son usados para recuperar del banco de modelos el

conjunto de rostros buscado. Para esto la imagen de prueba es primeramente

procesada por medio del conjunto de técnicas descritas en las secciones anteriores.

Cada VA es usado para extraer del mapa de memoria correspondiente los rostros que

produjeron dicho VA dando como resultado una lista de rostros candidatos. Esta lista es

finalmente reducida por medio de un mecanismo de umbralisado. Estas dos etapas son

enseguida descritas en más detalle.

Selección de candidatos:

Durante esta etapa, cada vector de atributos obtenido a partir de las características

visuales en una imagen de prueba es presentado al sistema. Si este vector es lo

suficientemente similar a uno de los aprendidos por la red neuronal (en términos de la

distancia euclidiana), entonces la salida correspondiente de dicha red será habilitada

seleccionado una fila de su mapa de memoria. Los votos ponderados en esa fila serán

enviados al registro de evidencia. Este proceso se repite para cada VA. Al final se

tendrá un conjunto de hipótesis arregladas como un histograma de pesos ponderados,

(ver figura). Este histograma se obtiene del registro de evidencias.

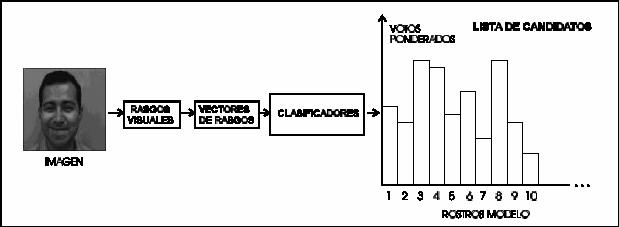
Figura 32. Selección de candidatos

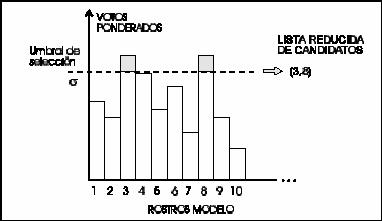
Figura 33. Reducción de candidatos

Reducción de candidatos.

Es claro que al final del proceso anterior se tendrá un histograma conteniendo los pesos

ponderados que cada rostro ha recibido durante dicho proceso (para un ejemplo, ver la

figura). Algunos rostros habrán recibido más votos que otros. Es necesario decidir

que rostros se aproximan lo más al rostro presente en la imagen. Intuitivamente,

aquellos rostros con más votos serán los mejores candidatos. Una manera de decidir

que objetos se encuentran presentes en la imagen consiste en usar un umbral de

selección, digamos . Así, aquellos rostros cuyos votos se encuentren arriba de serán

seleccionados como los mejores candidatos. Para decidir si un rostro se encuentra

presente en la imagen de entrada se usa el siguiente algoritmo:

H[i] contiene los votos ponderados recibidos por el rostro i durante el proceso de

extracción de candidatos y es el umbral de selección. En este trabajo, fue escogido

de forma que la lista final de candidatos contenga solamente los dos rostros con los

votos más altos. Esta selección dio resultados aceptables. Por ejemplo, la lista final contiene los rostros 3 y 8, lo cual significa que el rostro presente en la imagen es ya sea el 3 o el 8.

1.5.-Resultados experimentales y discusión

En esta sección, el desempeño de la arquitectura propuesta para el reconocimiento de

rostros es probado. Para esto se usa el conjunto de imágenes mostrado en la figura.

Figura 34. Un conjunto de imágenes de prueba.

1.6.-Entrenamiento de los clasificadores.

Para cada uno de los rostros mostrados en la figura 6, el conjunto de rasgos visuales

fue extraído según se explicó en la sección anterior. A partir de estos rasgos visuales, los vectores de atributos correspondientes fueron igualmente calculados. Estas cantidades permitieron entrenar cada uno de los clasificadores.

Como se explicó en la sección anterior, el valor de se escogió de forma que permitiera,

al mismo tiempo, diferenciar entre rostros de clases diferentes y agrupar rostros de la

misma persona. Para compensar variaciones en los "invariantes", se usaron 40

imágenes diferentes (4 para cada una de los 10 rostros). Estas fueron obtenidas al

colocar la cámara a diferentes distancias con respecto al sujeto, tratando de mantenerlo

siempre dentro del campo visual del sensor. Se le pidió girar un poco el rostro y

cambiar, a la vez, de expresión facial. Para cada una de las cuatro muestras seis

conjuntos de vectores de atributos fueron obtenidos dando como resultado un total de

240 vectores para entrenar los cuatro clasificadores.

1.7.-Reconocimiento.

Otras cien imágenes (diez por cada uno de los diez) diferentes a aquellas usadas

durante el entrenamiento fueron adquiridas. Estas fueron obtenidas de nuevo al situar la

cámara a diferentes distancias con respecto al sujeto, tratando de mantenerlo siempre

dentro del campo visual del sensor. De nuevo, se le pidió girar un poco el rostro

cambiando a la vez de expresión facial.

El número de veces (expresado en por ciento) que un rostro fue correctamente

reconocido se muestra en la tabla. Un rostro fue considerado como no reconocido si

este no estaba presente en la lista reducida de candidatos. De esta tabla se puede ver

que el desempeño promedio del sistema es del 87%.

Figura 35. Resultados experimentales

1.8.-Conclusiones y trabajo futuro.

Como conclusión, en este trabajo se presentó un sistema para el reconocimiento de

rostros a partir de una sola imagen en presencia de pequeñas deformaciones como

traslaciones, rotaciones, cambios de tamaño y diferentes expresiones faciales. La

arquitectura se compone de dos clasificadores cada uno compuesto, a la vez, de una

red neuronal estándar tipo ART 2 conectada a un Mapa de Memoria (MM). Las salidas

de los diferentes clasificadores están conectadas a un sumador (registro de evidencias)

común y a un conjunto de comparadores para la fusión de datos.

Durante una primera fase varios tipos de rasgos visuales fueron extraídos de una

imagen de un rostro. A partir de estos rasgos visuales varios vectores de atributos

fueron también obtenidos. Estos vectores de atributos fueron entonces usados para

entrenar los clasificadores correspondientes. Una vez entrenado el sistema, el proceso

de identificación es llevado a cabo. Este consiste de dos pasos. Durante el primer paso,

una lista restringida de las personas obedeciendo a una descripción de entrada es

obtenida en una primera instancia a la salida del registro de evidencias, en forma de un

histograma. Finalmente, durante el segundo paso, esta lista es reducida a través de un

método de umbral, para obtener la lista final de posibles candidatos correspondiendo a

la imagen de prueba. El desempeño de la arquitectura se probó con un conjunto

limitado de diez rostros. Los resultados fueron satisfactorios.

Una de las principales ventajas de este sistema reside en el hecho de que los rasgos

usados para calcular los vectores para describir un rostro son calculados a partir de

solo cinco puntos, lo cual simplifica bastante el procesamiento.

Actualmente, estan estudiando:

1) aumentando el número de rostros en el banco de datos para probar el desempeño del sistema en presencia de bases de datos más grandes, 2

2) adicionando más clasificadores para verificar si el desempeño del sistema mejora,

3) buscando un procedimiento automático para encontrar el óptimo para cada

3)clasificador.

4) tratando de extender la arquitectura propuesta para usar otro tipo de

4)datos personales como voz e información contenida en huellas dactilares, con el

4)objetivo de mejorar el desempeño del sistema. Nuestra meta consiste en extraer tan

4)rápidamente como sea posible del banco de modelos, una lista restringida de personas, de acuerdo a una descripción de entrada, cuando diferentes tipos de datos personales son presentados a la entrada del sistema.

1..9.-Referencias.

[1] M. Turk and A. Pentland, Face recognition using eigenfaces, Proc. of the IEEE

Conference on Computer Vision and Pattern Recognition, pp. 586-591 (1991).

[2] B. S. Manjunath, R. Chellappa and C. von der Malsburg, A feature based approach

to face recognition, Proc. of the IEEE Conference on Computer Vision and Pattern

Recognition, pp. 373-378 (1991).

[3] M. Kosugi, Robust identification of human face using mosaic pattern and BMP, Proc.

of the IEEE Workshop on Neural Networks for Signal Processing, 296-305, (1992).

[4] R. Brunelli and T. Poggio, Face recognition: features versus templates, IEEE Trans.

on Pattern Analysis and Machine Intelligence, 15(10):1042-1052, (1993).

[5] D. J. Beymer, face recognition under varying pose, Proc. of the IEEE Conference on

Computer Vision and Pattern Recognition, pp. 756-761 (1994).

[6] M. S. Kamel, H. C. Suen, A. K. C. Wang, T. M. Hong and R. I. Campeanu, Face

recognition using perspective invariant features, Pattern Recognition Letters, 15:877-

883, (1994).

[7] F. Gaudail, E. Lange, T. Iwamoto, K. Kyuma and N. Otsu, Face recognition system

using local autocorrelations and multiscale integration, IEEE Trans. on Pattern Analysis

and Machine Intelligence, 18(10):1024-1028, (1996).

2.- RECONOCIMIENTO DE FIRMAS USANDO REDES NEURONALES MULTICAPA

1.- INTRODUCCIÓN

El reconocimiento de firmas es un tema de investigación intensa debido a la gran importancia que tiene, entre otros aspectos, en el sistema financiero. Sin embargo no existe todavía un método suficientemente confiable, especialmente en la detección de firmas falsificadas. En este trabajo se desarrolla y evalúa un sistema de reconocimiento de firmas estáticas por medio de extracción de características (momentos de proyección, envolvente inferior, envolvente superior, envolvente lateral derecha y envolvente lateral izquierda) a partir de un arreglo de 5 redes neuronales Backpropagation extraídas de la firma estática. El sistema propuesto presenta mejor funcionamiento comparando con otros métodos, siendo además simple su realización. La comparación de los resultados obtenidos de este método con respecto a ADALINE muestran que la propuesta reconoció la totalidad de las firmas utilizadas para su evaluación. Mientras que ADALINE presentó una efectividad del 97.8%. Aunado a esto la Red propuesta es insensible al tamaño y la posición de la firma, características que la hace atractiva para aplicaciones practicas.

A través del tiempo se han desarrollado sistemas capaces de simular el comportamiento del cerebro humano en la realización de funciones especificas, siendo una de los más importantes paradigmas utilizados en las Redes Neuronales y la Inteligencia Artificial, que son una herramienta primordial para el desarrollo de sistemas para el reconocimiento de caracteres manuscritos, reconocimiento de voz, reconocimiento de rostros, reconocimiento de firmas y otras aplicaciones biométricas que han tenido éxito.

Para el reconocimiento de firmas se tiene principalmente los siguientes métodos: el reconocimiento en línea (el reconocimiento dinámico) y el reconocimiento fuera de línea (el reconocimiento estático). El sistema propuesto presenta mejor funcionamiento comparando con otros métodos propuestos teniendo además simple su realización.

2.- SISTEMA PROPUESTO

El sistema propuesto consiste en una etapa de extracción de envolventes y otra de la extracción de parámetros estadísticos. Seguido del entrenamiento en paralelo de cinco redes neuronales tipo BACKPROPAGATION, cada una de las cuales se entrenarán con los valores obtenidos de las envolventes superior, inferior, derecha e izquierda de la firma y la quinta red se entrenará con los valores obtenidos de los parámetros estadísticos, para finalizar se utilizarán los valores que arrojen las redes y se decidirá a quién pertenece la firma. El sistema propuesto se muestra en la figura.

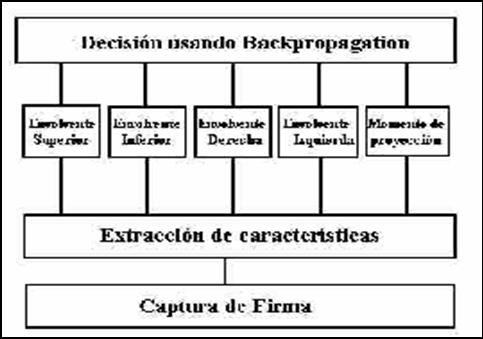
Figura 36. Sistema propuesto.

Extracción de envolventes

Una vez que las firmas han sido digitalizadas se procede a la extracción las envolventes superior, inferior, izquierda y derecha de la firma, y cada envolvente se divide en 12 partes, a cada una de ellas se le asigna un valor entero que representa la forma de la parte.

A continuación se presentan las envolventes superior, inferior, izquierda y derecha respectivamente de una firma separados en 12 partes con sus valores asignados.

El criterio que se tomó fue el siguiente:

0 No había píxeles en la submatriz

1 Había píxeles pero la información no formaba ningún valle, ni un pico

2 Se encontraba información en forma de pico

3 Se encontraba información en forma de valle

Figura 37. Firma capturada y difitalizada

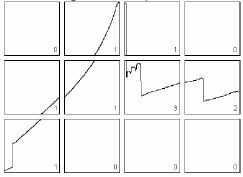
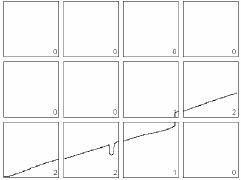
Figura 38. Envolvente 1 Figura 39. Envolvente 2

Figura 40. Envolvente 3 Figura 41. Envolvente 4

Parámetros estadísticos

Con el método utilizado para extraer los parámetros estadísticos se obtienen valores de Kurtosis, valor Skewness, [1] valor relativo entre Kurtosis y Skewness y valor relativo entre proyección vertical y proyección horizontal de la firma bajo análisis.

3.-RESULTADOS OBTENIDOS

Para evaluar el sistema propuesto, se generó un base de datos que consiste de 130 firmas (15 firmas de 9 personas), 90 firmas (10 firmas de 9 personas) son usados para entrenar las cinco redes separadamente, 45 firmas (5 firmas de 9 personas) son usados para evaluación de

funcionamiento del sistema propuesto. Los resultados de la simulación computacional realizados en una Workstation Kayak XA mostraron que aproximadamente el 100 por ciento de las firmas se reconoce correctamente. Los factores importantes para reconocimiento son sobre todo la envolvente superior, envolvente derecha y parámetros estadísticos de la firma. Estas características contribuyen más que la envolvente inferior e izquierda al funcionamiento de reconocimiento de la firma, puesto que tiene menos información.

4.-REFERENCIAS

[1] R. Bajaj and S. Chaudhury, "Signature Verification Using Multiple Neural Classifiers", Pattern Recognition, vol. 30, No. 1, Pag. 1-7, 1997.

[2] F. Leclerc and R. Plamondon, "Automatic Signature Verification: The State of the Art 1989- 1993", International Journal of Patter Recognition and Artificial Intelligence Vol. 8, No. 3 , Pag. 643-660, 1994.

[3] M. Ammar, "Progress in Verification of Skillfully Simulated Handwritten Signature", International Journal of Patter Recognition and Artificial Intelligence, vol. 5, No. 1 & 2, pag. 337-351, 1991.

[4] K. Toscano M., G. Sánchez P., M. Nakano M. y H. Pérez M., "Reconocimiento de Firmas por Medio de Extracción de Características", Proc. of 2nd. International Congress of Research in Electrical and Electronics Engineering, CIIIEE'98, Sep. 98.

3.- RECONOCIMIENTO DE PATRONES A PARTIR DE IMÁGENES AÉREAS.

1.-INTRODUCCIÓN.

La fotointerpretación es una herramienta útil para reconocer patrones y realizar diversos tipos de Planificación Territorial a partir de fotografías aéreas. Hasta ahora, el trabajo de fotointerpretación se realiza con la participación de expertos humanos. El desafío consiste en incorporar, paulatinamente, el computador en esta tarea. El presente trabajo, plantea realizar una clasificación de coberturas de terreno a partir de fotografías aéreas digitalizadas utilizando para tal efecto las redes neuronales de aprendizaje supervisado y

no supervisado. Los métodos desarrollados en el presente, se extienden fácilmente para el estudio de imágenes satelitales multiespectrales.

El reconocimiento de patrones es aquella disciplina científica cuyo objetivo es la clasificación de objetos en un número dado de categorías o clases (Theodoridis & Koutroumbas, 1998). En el tipo de aplicación que nos corresponde en este articulo, estos objetos a clasificar son porciones de imágenes. Las imágenes provienen de fotografías aéreas tomadas de determinadas regiones. En el caso presente son fotografías del Área de Manejo Integrado Cota-Pata en el departamento de La Paz, Bolivia.

Figura 42. Fotografía aérea del parque Cota-Pata de Bolívia

Como se observa en la figura las diferentes coberturas del terreno dan diferentes patrones de textura. La clasificación y cuantificación de estos patrones a partir de las fotografías aéreas tiene importancia en la construcción de mapas temáticos y se viene realizando hace algunas décadas. Pero la década de los 80 y los 90 fueron especialmente exigentes por la creciente necesidad del estudio de la Biodiversidad y con esto la

creación de Parques Nacionales o Reservas que posean una diversidad de ecosistemas y hábitats. Paralelamente, el desarrollo de la tecnología computacional abarató los costos y fue posible preguntarse sobre la factibilidad de incorporar a la máquina y sus potencialidades en los procesos de clasificación de la cobertura del terreno, usando como insumos las fotografías aéreas con el propósito de realizar mapas de la

cobertura y establecer pautas para la cuantificación de la diversidad de las regiones con el fin de generar información útil para su manejo sostenible.

2.-PAUTAS PARA LA CONSTRUCCIÓN DEL SISTEMA DE CLASIFICACIÓN

La computadora trabaja con imágenes digitales. Una imagen digital resulta de la discretización de una imagen continua I(x,y). La imagen continua puede ser la fotografía aérea, después del proceso de discretización se obtiene la imagen digital I(m,n), con

que se almacena en un arreglo bidimensional de orden MxN. La intensidad de la imagen es cuantificada en G niveles de gris. De esta manera cada elemento (m.n) puede tomar un valor entre 0, 1, ...., G-1. Es común que G = 2p ; donde p = 1,2, 3,...

El ojo humano puede distinguir cerca de 16 niveles de gris pero la máquina generalmente trabaja con G = 256. Aquí puede radicar la posibilidad de crear un sistema de clasificación competitivo con el sistema de clasificación humano. Dentro el arreglo bidimensional cada elemento ó pixel se representa de diferente forma. Por ejemplo, puede ser un real de doble precisión (64 bits), ó un entero positivo (8 bits). Para el tratamiento digital se emplean generalmente cuatro tipos de imágenes:

1. Las imágenes indexadas que consisten de dos arreglos, la matriz de la imagen y la matriz del mapa de colores. Este último es un conjunto ordenado que permite codificar los colores presentes en la imagen.

De esta manera, el valor de un elemento en la matriz de la imagen denota a un código en el mapa de colores. Este código contiene tres valores en el sistema RGB, por eso, el mapa de colores no es más que un arreglo que en cada fila contiene tres elementos que codifican un color en el sistema RGB, estos elementos pertenecen al intervalo [0,1].

2. Las imágenes de intensidad consisten de un solo arreglo bidimensional, cada elemento del arreglo tiene un valor que cae dentro del intervalo [0,1] ó dentro del intervalo [0,255] comúnmente el valor cero representa el negro y el valor 255 el blanco.

3. Las imágenes Binarias son estructuralmente muy parecidas a las imágenes de intensidad, la diferencia radica en que los elementos de la imagen solo pueden tomar dos valores, ceros o unos.

4. Las imágenes RGB se almacenan en un arreglo tridimensional cuya la tercera dimensión sirve para almacenar la codificación RGB.

Existen muchos formatos comerciales para el almacenamiento de las imágenes, entre estos: BMP, JPG, PCX, TIFF. En el presente artículo se trabajará preferentemente con imágenes del tipo BMP que se almacenan en la memoria como imágenes de intensidad. De esta manera, la fotografía de una región se almacena en el computador como la imagen base. De esta imagen se extraerán algunas porciones que representan los patrones a clasificar. En la fig. 5.2 se muestra la imagen y algunas porciones que visualmente son diferentes por pertenecer a diferentes clases de cobertura del terreno. La idea radica en construir una Red Neuronal que permita clasificar estas porciones (patrones) en forma automática dentro de un número dado de clases.

Figura 43. Diferentes coberturas del terreno extraídas de la fotografía digital

Para esto, es necesario encontrar unas características medibles que posibiliten la diferenciación de clases y que compitan con la fácil diferenciación visual que se puede realizar. La máquina es buena manejando números pero no así formas ni texturas. Supóngase que se han encontrado l características representadas por las variables xi, i = 1, 2, ....... l, agrupando estas variables se obtiene el vector de

características.

x = [x1, x2, ....... , xl] T

De esta manera, cada clase quedará asociada a unas variaciones aleatorias de este vector. Por

ejemplo, el patrón bosque estará asociado a variaciones del vector x que contiene las características que aún

permiten diferenciar el bosque de otras clases de cobertura del terreno representadas en la fotografía aérea.

Para el mejor desempeño de un sistema clasificador se hace necesario añadir dos categorías a los tipos de

cobertura que queremos clasificar, estas son: C confusos, C desconocidos. Estas dos categorías adicionales liberan al

sistema clasificador de dar respuestas concluyentes cuando existe confusión y evitan la excesiva

generalización al clasificar una textura que no corresponde a una cobertura de terreno.

Como se dijo antes, un examen visual de la fotografía aérea permite notar que diferentes coberturas de terreno representan diferentes texturas en la imagen. ¿Cómo se puede obtener características cuantitativas que permitan diferenciar una textura de otra?. La respuesta no es trivial, y depende fuertemente de las condiciones y limitaciones de una aplicación concreta para la cual se diseña el sistema de clasificación. Un principio orientador puede sugerir encontrar características cuyos cálculos no consuman excesivos esfuerzos computacionales. Según (Theodoridis & Koutroumas, 1998) el diseño completo de un sistema de clasificación atraviesa etapas que mostramos a continuación:

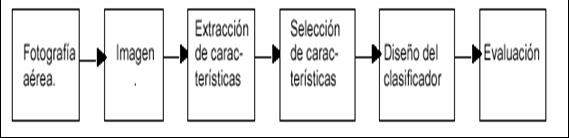Figura 44. Estapas.

Uno de los principales problemas que se debe resolver en la clasificación es la dimensión del vector de características. En una imagen, el número de características puede ser tan grande como el número de pixeles (en un patrón de 50 x 50 pixeles la dimensión del vector de características sería 2500). Debido a esto, surge la necesidad de reducir esta dimensionalidad, buscando por un lado la optimización del tiempo de cálculo y por otro lado evitando la redundancia al tratar con características altamente correlacionadas.

Según Bishop (1995), el procedimiento para la selección de características tiene dos componentes. Primero, se debe tener claro un criterio que permita juzgar por qué un subconjunto de características es mejor que otro subconjunto. Segundo, debe existir un procedimiento sistemático para encontrar estos subconjuntos de características. Una búsqueda ciega a partir de d-características necesitaría buscar en un espacio con 2d elementos, lo cual es impracticable para valores altos de d, por ejemplo, si d=100. Si de alguna manera se decidió que se necesita f d características. En este caso el espacio de búsqueda tiene el número de elementos igual a:

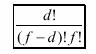
Que en general es más pequeño que d.

Son buenas aquellas características que tienden a alargar la distancia entre clases y a disminuir la distancia dentro de las clases. O en otras palabras, la esperanza radica en encontrar características que generen grandes variaciones entre clases y pequeñas variaciones dentro de las clases. La fig. 5.4 muestra algunos posibles casos que pueden ocurrir con la selección de características, lo ideal es encontrar características que generen pequeñas distancias dentro de las clases y grandes distancias entre clases.

Figura 45.

Clasificación de puntos en el espacio euclidiano: a) pequeña distancia entre las clases y pequeña distancia dentro de las clases; b) mucha distancia dentro de las clases y pequeña distancia entre las clases; y, c) Mucha distancia entre las clases y poca distancia dentro de las clases.

Es bueno recalcar que una imagen del mundo real tiene generalmente demasiada redundancia, fundamentalmente por que los objetos tienen una estructura estable que permite reconocerlos a pesar de la presencia de ruido. Por eso, en una imagen, afortunadamente, no es necesario elegir todos los pixeles como entrada a una red neuronal pues existe demasiada redundancia en esta Información. Una forma de eliminar la redundancia es realizar la Transformada de Fourier y eliminar los componentes con energía débil. También pueden ser usadas otras transformadas basadas en las de Fourier como la Transformación Discreta de Wavelets. Sin embargo, el propósito del presente trabajo es encontrar características que exijan un bajo consumo de cálculo en comparación a lo exigido por estas transformaciones. Aún cuando, la porción del patrón a reconocer sea pequeña, digamos 50x50, el número de pixeles presente será de 2500. Este número es muy grande para implementarlo en un sistema de clasificación del cual se espera un buen desempeño en la generalización. Por lo tanto, en el presente trabajo se recurrió al uso de la textura como una propiedad diferenciadora de las clases de cobertura de terreno presentes en la fotografía aérea. La textura de un patrón está caracterizada por la forma en que están distribuidos espacialmente los pixeles con sus diferentes niveles de gris. Aunque esta definición no es muy formal, es conceptualmente suficiente como para buscar características cuantitativas sobre la base de explotar las relaciones de los pixeles dentro del patrón.

Junto con las transformaciones arriba mencionadas se pueden usar características que surgen del tratamiento estadístico de la distribución de pixeles dentro del patrón. De estas se usan principalmente las siguientes (Theodoridis & Koutroumbas, 1998).

Aunque, existen diversos métodos para la selección de características, que pueden estar basados en criterios estadísticos, en el presente trabajo se usa el conocimiento heurístico basado, por ejemplo, en el hecho de que las características deberían ser invariantes a la rotación porque un bosque sigue siendo un bosque independiente del punto de vista del observador. En general la textura no cambia a la rotación, y es la textura el patrón que precisamente se pretende clasificar. Entre las características seleccionadas se pueden

indicar:

1. El valor medio de la intensidad del patrón

2. La dispersión.

3. El número de cambios de la intensidad por filas.

4. El número de cambios de la intensidad por columnas.

En la implementación del trabajo se creyó conveniente complementar las anteriores características con una selección al azar de algunos pixeles del patrón. Una vez que las características han sido seleccionadas, estas pueden tener un rango diverso de valores. Para la mayoría de las aplicaciones es conveniente transformar los datos de modo que el proceso de cálculo mantenga propiedades de estabilidad. En el caso más sencillo, estas

transformaciones son lineales respecto a los datos de entrada, y a veces también a los de salida. A este proceso se le llama Normalización.

Si se tienen N datos disponibles para las características xk, podemos calcular la normalización como:

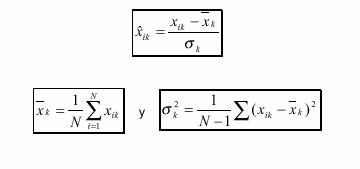
CLASIFICACIÓN SUPERVISADA

En esta clasificación, todo el diseño se basa en la existencia de un conjunto de datos de

entrenamiento que a priori están clasificados. Y el sistema en consecuencia explota este conocimiento.

En el presente trabajo el método supervisado parte de un cierto conocimiento previo del terreno, adquirido por experiencia previa o por trabajos de campo.

La Red de retropropagación.

En 1986, Rumelhart, Hinton y Williams, basados en otros trabajos formalizaron un método para que una red neuronal aprendiera la asociación que existe entre los patrones de entrada a la misma y las clases correspondientes, utilizando más niveles de neuronas que los que utilizó Rosenblatt para desarrollar el Perceptrón (Hilera et al., 1995). Este método conocido como retropropagación (Backpropagation), está basado en la generalización de la regla delta y a pesar de sus propias limitaciones, ha ampliado de forma considerable el rango de aplicaciones de las redes neuronales.

Los algoritmos de clasificación estadística son los más comunes para las técnicas de teledetección y generalmente están ampliamente tratados en varios libros. Estos métodos de clasificación son referidos como clasificadores específicos de pixel o punto (Richards, 1995) en el que se etiqueta un pixel sin tomar en cuenta de cómo están etiquetados los pixeles vecinos. Este conocimiento de la relación existente entre pixeles

vecinos es una rica fuente de información que no es explotada en un clasificador simple y tradicional. Se considerará la importancia del contexto espacial que genera la textura y se mostrarán los beneficios de tomarla en cuenta cuando se realicen decisiones de clasificación.

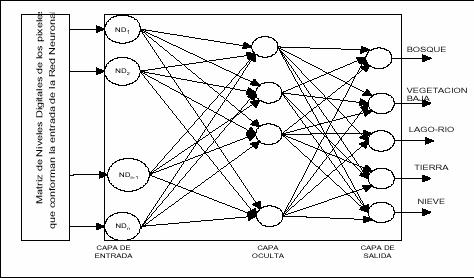
Figura 46.

Arquitectura de la Red

La arquitectura de la red neuronal artificial es de conexiones hacia delante y multicapa con función de activación sigmoidal. El modelo de la red estará conformada por una capa de entrada, una capa oculta y una capa de salida con M neuronas correspondientes a las categorías definidas como: Bosque, Vegetación baja, Lago - Río, Tierra y Nieve, como se muestra en la figura.

Fase de entrenamiento

Para comenzar el proceso de entrenamiento, es necesario realizar una identificación de las categorías a clasificar. Luego de identificar las áreas, se procede al proceso de enseñanza de la red. El funcionamiento es el siguiente:

Para el proceso de entrenamiento se crea un archivo que contiene los parámetros de entrada y la salida deseada de la red. Se realiza una lectura del archivo y se ejecuta el aprendizaje hasta que el error de la red sea aceptable. Este proceso está incluido dentro del sistema de clasificación NAIRA (se recomienda realizar los experimentos necesarios con el programa propuesto).

Fase de clasificación o reconocimiento

Cuando el proceso de entrenamiento de la red termina aceptablemente para cada patrón deseado, se puede realizar una fase de clasificación "mostrando" a la red las categorías que se desea que reconozca. Estos patrones pueden ser los que se utilizaron durante el proceso de enseñanza o nuevos que la red nunca antes había visto. Esto es una de las características más frecuentes de las redes neuronales: la generalización.

Durante las pruebas experimentales, se pudo evidenciar que si una red deja de aprender antes de llegar a una solución aceptable, se debe realizar un cambio en el número de neuronas ocultas, el sesgo del modelo (c), el coeficiente de aprendizaje (), o simplemente, volver a empezar el entrenamiento con un conjunto distinto de pesos.

El programa NAIRA puede ser obtenido

de http: //otilio.dcs.fi.uva.es/airene/Software/bp/En la figura se muestra una de las pantallas del programa que despliega el resultado de la clasificación de una porción de la fotografía aérea.

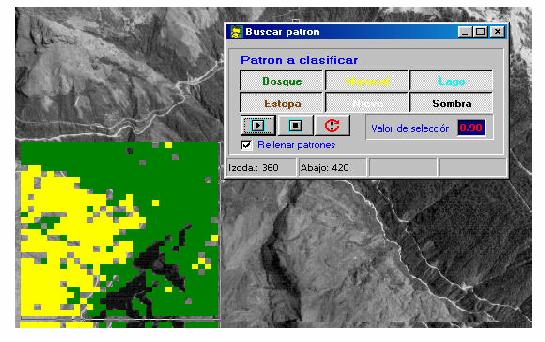
Figura 47.

CONCLUSIONES

Se ha demostrado que se puede aplicar un modelo de red neuronal artificial para el reconocimiento de patrones en fotografías aéreas, aportando de esta manera con una nueva herramienta para realizar fotointerpretación y su posterior tratamiento. También se ha demostrado que para realizar una clasificación, no se puede ignorar la "vecindad" o el contexto alrededor de un pixel, es decir, un solo elemento no brinda toda la información acerca de una categoría.

Una característica frecuente de las redes neuronales de conexiones hacia delante que utilizan retropropagación, es la generalización. Se pudo comprobar durante las pruebas experimentales la aparición de esta característica sobre información que no habían ingresado durante la etapa de entrenamiento, pero fue solucionada utilizando un valor umbral subjetivo. Es decir, debido a que la función de activación brinda una salida entre 0 y 1 para algún patrón, en la fase de reconocimiento, para alguna información de entrada se calculan las salidas yk , sólo si existe una única salida que sea mayor o igual al umbral sugerido se considera como un reconocimiento aceptable, si existe mas de una salida con valor mayor o igual al umbral, se tienen salidas o clases parecidas o confusas y, si todas las salidas no superan este umbral se tiene el caso de patrón desconocido.

El modelo de RNTF planteado demuestra robustez en el estudio del reconocimiento de patrones, la teoría que propone no se considera la panacea pero muestra resultados que son alentadores en el diseño de cerebros artificiales o modelos de redes neuronales más naturales. El ejemplo probado en este trabajo se puede extender para desarrollar la percepción de robots mediante visión para la actuación en entornos dinámicos.

RECOMENDACIONES

Como recomendaciones se sugieren las siguientes:

1. Dependiendo del tipo de aplicación, una matriz de 15x15 pixeles (225 neuronas) para el trabajo, es suficiente para realizar un reconocimiento de categorías. Si se desea realizar un "buscador" de patrones,se puede disminuir hasta 10x10 pixeles dependiendo al patrón de búsqueda.

2. Si bien las redes neuronales cumplen muy bien su trabajo y tienen una amplia gama de aplicaciones sobre varios dominios, tienen algunas limitaciones. Por ello han aparecido recientemente distintas extensiones de estos modelos, como por ejemplo, las redes de alto orden, las redes neuronales probabilísticas, las redes neuronales difusas y las redes neuronales basadas en "Wavelets" y redes funcionales [Castillo et al. 1999].

3.Realizar un análisis multiespectral sobre imágenes satelitales, tomando en cuenta el contexto (no un clasificador específico de pixel o punto). Esto incrementa la cantidad de información de entrada muy necesaria para realizar una discriminación entre patrones.

BIBLIOGRAFÍA

[ATRÁS]

Aguilar, R. "Red Neuronal de Topología Flexible". En: VI Congreso Nacional de Ciencias de la Computación, La Paz, Bolivia. Septiembre de 1999.

Bishop, C. M. “Neuronal Networks for Pattern Recognition”, Clarendon Press, Oxford, 1995.

Michell. Capitulo 4: Artificial Neural Networks.

Gonzales Woods. “Tratamiento Digital de Imágenes”.

B. Martín del Brío, A. Sanz Molina. “Redes Neuronales y Sistemas Borrosos”, RA-MA, 1997.

James A. Freeman, David M. Skapura. “Redes Neuronales. Algoritmos, aplicaciones y técnicas de programación”. ADDISON-WESLEY/DIAZ DE SANTOS, 1993

[Haykin-94] Haykin, S. “Neural Networks: A Comprehensive Foundation”. Macmillan, 1994.

https://www.gc.ssr.upm.es/inves/neural/ann2/